Math 181A

Calculus and Analytic Geometry II

Fall 2009

Homework assignments

Daily notes

Reading period and exam week

Our final exam is scheduled for 8:00--10:00 am on Wednesday, December 16 in our usual classroom. The final exam will cover all of the material we have studied this semester. You can bring one page (standard notebook size) of notes to use on the final. You can use both sides of the page. I will not provide formulas such as the list of derivatives we've used for previous exams.

Here is a master list of objectives for the course. This is a complilation of objectives from individual exams with a few redundancies removed.

Below is a list of times I currently plan to be available. I may need to update this if other commitments arise.

Help is also available in the CWLT during the following times:

Chuck Hommel is the math department faculty member assigned to the CWLT. Betsey Kersey is a senior math major who has a lot of tutoring experience.

Tuesday, December 8

Monday, December 7

Here are notes we went over in class on logistics for the next two weeks:

• Exam #4 is on Tuesday December 8 from 8:00 to 9:20 am. The exam will cover material from Sections 7.7 and 8.1--8.9 with the exception of the first part of Section 8.9.
• I have reserved TH 383 for a study session this evening (Monday December 7) starting at 7:30 pm.
• I will have Exam #4 available for you to pick up on Monday December 14 at the latest. I will send an e-mail when I have finished grading the exam.
• Our final exam is scheduled for 8:00--10:00 am on Wednesday, December 16 in our usual classroom. The final exam will cover all of the material we have studied this semester.
• You can bring one page (standard notebook size) of notes to use on the final. You can use both sides of the page. I will not provide formulas such as the list of derivatives we've used for previous exams.
• By Friday December 11, I will make a master list of course objectives available on the course web page.
• I will be available on Thursday and Friday of reading period and during exam week. I'll post a schedule of my availability each day on the course web page.
• When I finish grading Exam #4, I will update data for the on-line score check feature on the course web page. I'll update it again once I have finished grading your projects and final exam. If you see any discrepancy between what I have recorded and what you have or recall, let me know as soon as possible.

Friday, December 4

Exam #4 will be on Tuesday December 8 from 8:00 to 9:20 am. It will cover material from Sections 7.7 and 8.1 through 8.9 of the text. You are not responsible for Taylor's Theorem and The Remainder Estimation Theorem in Section 8.9. This handout has a list of specific objectives.

Here's the problems from the Fall 2005 Math 122 exams that are most relevant to our Exam 4 on Tuesday:

• #1,4,5,6,7 from Exam 3 (Fall 2005 Math 122)
• #1-7 from Exam 4 (Fall 2005 Math 122) plus the option in parentheses from #8

The final exam will be Wednesday December 16 from 8:00 to 10:00 am.

Thursday, December 3

Note: I will not be available for appointments tomorrow afternoon and will have only very limited time in the morning. Today, I have office hour from 1:00 to 2:30 and will be available for appointments until 4:00.

Our main topic for the past few days has been Taylor polynomials and Taylor series. These are related in that a Taylor series is the limit of Taylor polynomials as the order goes to infinity. A Taylor polynomial can be used to approximate a function. A Taylor series gives an exact power series representation of a function. In class today, we looked at two examples of how power series representations can be useful. The second example (from this handout) resulted in Euler's formula:

We were able to deduce this unexpected (and very useful) relationship because power series representations allowed us to work with the exponential, sine, and cosine functions in a unified framework.

Quiz #3 will be tomorrow. It will be very similar to Practice Quiz #3. For Quiz #3 and Exam #4, you are expected to know the Taylor series results for the exponential function, sine, and cosine along with the geometric series result:

Exam #4 will be on Tuesday December 8 from 8:00 to 9:20 am.

The final exam will be Wednesday December 16 from 8:00 to 10:00 am.

Tuesday, December 1

In class, we looked at several ways to get a power series representation of a given function. Our options include

• directly computing the Taylor series coefficients
• substituting into a known power series representation
• differentiating or antidifferentiating a known power series representation

We did not get to an example of this third option in class. This handout has an example of antidifferentiating a known power series representation to get a new power series representation. We will briefly talk about this in class on Thursday.

Quiz #3 will be on Friday. It will be very similar to Practice Quiz #3.

For Quiz #3 and Exam #4, you are expected to know the Taylor series results for the exponential function, sine, and cosine along with the geometric series result.

Monday, November 30

In class, we introduced the idea of Taylor series. A Taylor series is a power series with coefficients based on the derivatives of some given function f(x). In the most common cases, the Taylor series computed this way will converge to the function f(x) on the interval of convergence for the series.

The example we did in class produced a Taylor series starting with the exponential function f(x)=e^x. As we will see, this Taylor series converges to the exponential function for all x. That is,

We'll soon find power series representations of other familiar functions such as sine and cosine. Power series representations give us a unified view of functions that have disparate origins. This unified view will reveal some interesting connections. For example, we will see that the exponential function can be related to the sine and cosine function.

For reference, here are solutions to Quiz #2 and a solution for Section 8.6 Problem 26. Keep in mind that there may be other reasonable approaches to these problems.

Quiz #3 will be on Friday, December 4. I'll post a practice exam here sometime tomorrow.

Exam #4 will be on Tuesday December 8 from 8:00 to 9:20 am.

The final exam will be Wednesday December 16 from 8:00 to 10:00 am.

Tuesday, November 24

In class today, we looked at examples of how to determine the interval of convergence for a power series. For a power series ∑c_nxⁿ, the interval of convergence consists of an interval centered at x=0 possibly including one or both of the endpoints. For a power series ∑c_n(x-a)ⁿ, the interval of convergence consists of an interval centered at x=a possibly including one or both of the endpoints.

Below are plots of partial sums for the power series examples we looked at in class yesterday. Each new frame of the animation shows a partial sum with one additional term. These particular examples happen to converge to familiar functions: sin(x), cos(x), e^x, and 1/(1-x). After Thanksgiving break, we'll see how to start with a function and then build a power series expansion equal to that function.

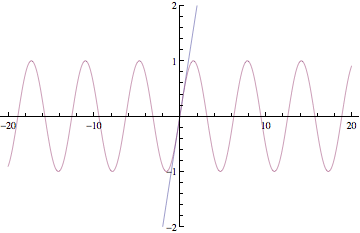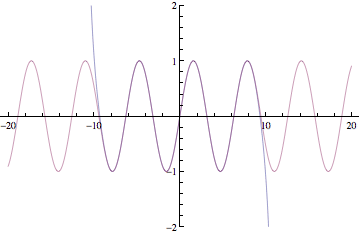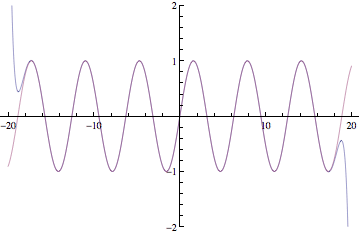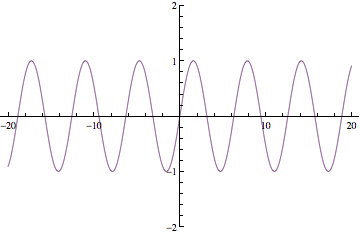
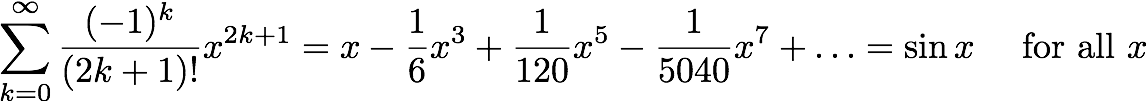
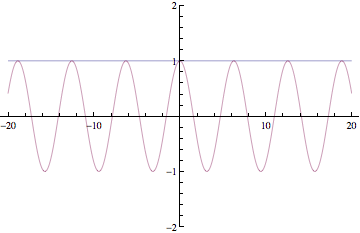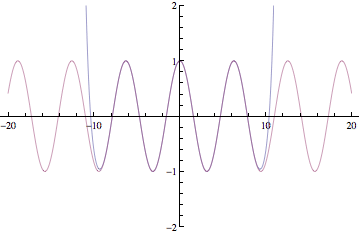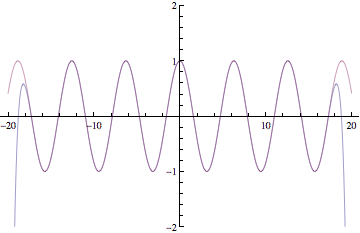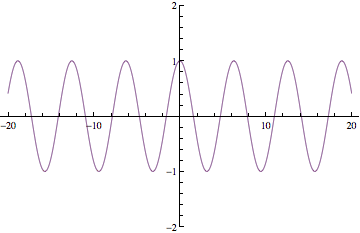
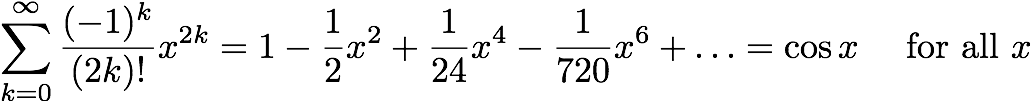
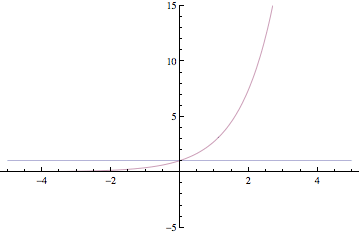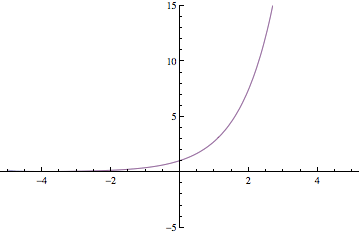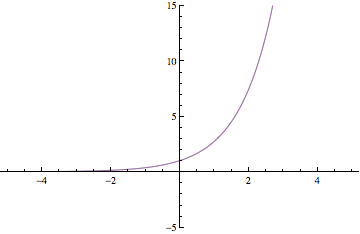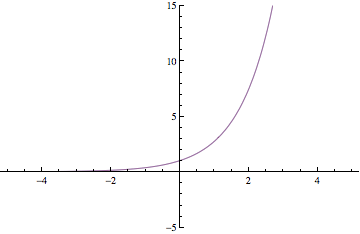
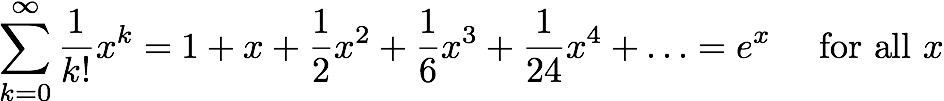
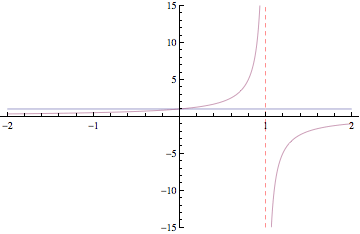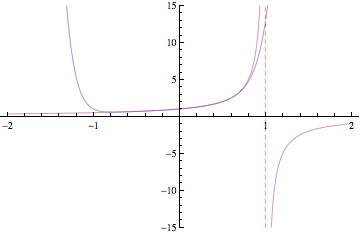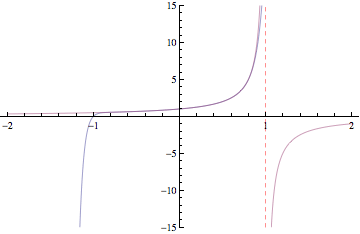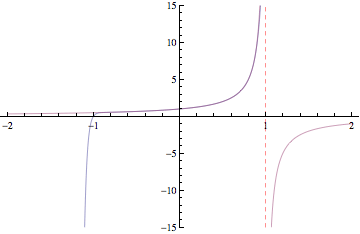
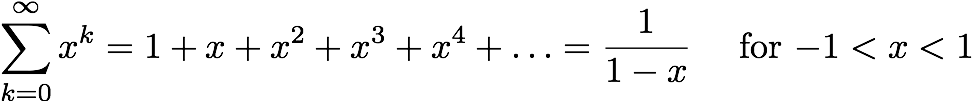
Have a great break!

Monday, November 23

In class, we started discussing power series by looking at specific examples that happen to be related to familiar functions (namely, sine, cosine, and the exponential function). Roughly speaking, a power series is a "polynomial of infinite degree" in some variable. So, a power series in the variable x is a series ∑c_kx^k in which each term is the product of a coefficient c_k and the corresponding power x^x. Since the series is expressed in terms of a variable x, the series may converge for some values of x and diverge for other values of x. So, given a power series, the central question we ask is For what values of x does the power series converge?

In the next day or two, I'll post some plots similar to the ones we looked at in class. I'll also provide a link so you can download the Mathematica from class so you can experiment if you want.

I have not yet assigned problems from Section 8.7. I'll do so after tomorrow's class.

Quiz #2 will be tomorrow (Tuesday November 24). It will be very similar to Practice Quiz #2.

Friday, November 20

Up to now, the arguments and tests we developed for series apply only to series with terms nonnegative. Today, we looked at some examples of series that have a mix of positive and negative terms. In general, analyzing these series is more difficult. We will not develop tools for all such series, but we do have two special cases:

• If a series has terms that alternate positive and negative, we can check if the conditions of the alternating series theorem hold. If so, we can conclude that the series converges. If not, we would need some other way to analyze the series.
• For a series ∑a_k, we can analyze the related series ∑|a_k|. It is a fact that if ∑|a_k|converges, then ∑a_k converges. Since all of the terms in ∑|a_k| are nonnegative, we can use our tools (integral test, comparison arguments, ratio test) in analyzing ∑|a_k|.

Here's some language that goes along with the second case: If ∑|a_k| is convergent, we say that the original series ∑a_k is absolutely convergent. So, the main result in the second case tells us that if a series is absolutely convergent, then the series is convergent.

Quiz #2 will be on Tuesday November 24. It will be very similar to Practice Quiz #2.

Thursday, November 19

We started class by looked at Section 8.1 #66 as an example of where calculator round-off error can be misleading if you are looking at numerical evidence to make a conjecture about a sequence limit.

The main new idea from today's class is the ratio test. The main idea of the ratio test is to check whether or not a series ∑a_k is essentially geometric in the "tail" of the series. A series is geometric if successive terms have a constant ratio. For a series ∑a_k, the ratio of successive terms is a_k+1/a_k. If the limit as k→∞ of a_k+1/a_k exists, then the ratio of successive terms is getting close to that constant limit for large values of k. If so, the "tail" of ∑a_k is essentially geometric. If that ratio is less than 1, the series is convergent. If that ratio is greater than 1, the series is divergent.

The ratio test gives us a true test in the sense that we can apply it to a series without knowing in advance what the result is. In contrast, what are commonly called comparison "tests" are not true tests. Rather, comparison "tests" are a style of argument that allows us to rigorously justify a conclusion. But, we need to use our intuition and informal reasoning to generate a conjecture before we can put together a comparison argument since putting together an argument requires us to bring in a comparison series of the right flavor (convergenet or divergent).

Section 8.5 discusses the ratio test. A second test, the root test is also discussed. We will not cover the root test. For reference, here's a brief description. In a geometric series ∑x^k, the ratio of successive terms is given by x. Note that this ratio is the kth root of the kth term: (x^k)^1/k=x. So, we can check if a non-geometric series ∑a_k is essentially geometric in the "tail" by looking at the kth root of the kth term as k→∞. That is, we analyze the limit as k→∞ of (a_k)^1/k. If this limit exists and is less than 1, then the series ∑a_k is convergent. If this limit exists and is greater than 1, then the series ∑a_k is divergent.

I have assigned problems from Section 8.5 that you should be able to do using the ratio test (or other tools we've developed) but not requiring the root test.

We will have two more in-class quizzes before Exam #4:

• Quiz #2 on Tuesday, November 24 covering ideas from Sections 8.1 through 8.5.
• Quiz #3 on Friday, December 4 covering ideas from Sections 8.6-8.9

Before each quiz, I'll give you a practice quiz that will have the same type of question as the actual quiz. Here's Practice Quiz #2.

Exam #4 will be on Tuesday, December 8. It will cover material from Section 7.7 and Chapter 8.

Tuesday, November 17

A series for which the sequence of terms converges to 0 can be either convergent or divergent. The rate at which the terms go to 0 is crucial. Limit comparison arguments are a way of comparing the rate at which one sequence of terms {a_k} goes to 0 with the rate at which some other sequence of terms {b_k} goes to 0. We have three possibilities:

• a_k/b_k→0 which tells us that the a_k go to 0 fast in comparison to how the b_k go to 0
• a_k/b_k→L with 0<L<∞ which tells us that the a_k go to 0 at the same rate in comparison to how the b_k go to 0
• a_k/b_k→∞ which tells us that the a_k go to 0 slowly in comparison to how the b_k go to 0

We can use these to reach a conclusion about the convergence of the series ∑a_k if we know about the convergence of the series ∑b_k. Here's the possibilities:

• If a_k/b_k→0 and ∑b_k converges, then ∑a_k converges.
• If a_k/b_k→0 and ∑b_k diverges, then no conclusion about ∑a_k can be reached by this comparison.
• If a_k/b_k→L with 0<L<∞, then ∑a_k and ∑b_k either both converge or both diverge.
• If a_k/b_k→∞ and ∑b_k diverges, then ∑a_k diverges.
• If a_k/b_k→∞ and ∑b_k converges, then no conclusion about ∑a_k can be reached by this comparison.

I have assigned problems from Sectoin 8.4 including two problems to submit on Friday.

Quiz #1 will be on Thursday. It will be identical to Practice Quiz #1 from Monday's class.

For those planning to take MATH 280 next spring, note that we have opened a third section of the course. Check Cascade for the details.

Monday, November 16

We started class today with Practice Quiz #1. We'll start class on Thursday with a "live" version of this quiz. This will be the first of two or three in-class quizzes we will have before Exam #4. If your overall percent score on these quizzes is higher than your percent score on Exam #4, then your Exam #4 percent score will be replaced by a weighted average of the exam percent and quiz percent with the exam percent weighted at 85% and the quiz percent weighted at 15%. If your overall percent score on the quizzes is lower than your percent score on Exam #4, then your Exam #4 score will not be changed. So, the quiz scores will, at worst, have no effect on your Exam #4 score.

The main purposes of these quizzes are to enourage you to master new concepts in a timely fashion and to give you feedback on your level of mastery. The material we are dealing with builds in a hierarchy. Mastering the fundamentals along the way is necessary to reach the end of the story with a sufficient level of understanding.

I'll determine a specific schedule for the quizzes and post that schedule here tomorrow.

In class, we began looking at comparison arguments. The goal of a comparison argument is to justify a conclusion about convergence/divergence of a given series ∑a_k by making a comparison to another series ∑b_k for which we already have a conclusion about convergence/divergence. I've assigned a few probems from Section 8.4 that you can analyze using the tools we've developed so far. Tomorrow, we'll talk about limit comparison arguments. These provide a more general way of making a comparison between a given series and a chosen series than the direct comparison arguments we used in class today.

Friday, November 13

In class, we continued our discussion of series. So far, we have established that the sum of 1/k diverges and the sum of 1/k² converges (with a sum less than 2). These two series are examples of p-series. To establish each of these results, we set up a comparison to a related improper integral for which we already knew convergence/divergence. We have also established that the sum of x^k converges if and only if |x|<1. Furthermore, we established that the sum is 1/(1-x) (provided we start with k=0). These series are called geometric series. Next week, we'll look at more general series. We will often establish convergence or divergence by comparison with a p-series or a geometric series.

Geometric series are covered in Section 8.2 of the text. P-series are discussed in Section 8.3 of the text. I've assigned problems from both of these sections.

There are some useful features on your TI-8X for working with sequences and series. For the TI-83/84, you can read a nice introduction to these at this TI tutorial. This specific tutorial is part of a larger online course on using a TI-83/84 for calculus that might be of general use.

You can also use Mathematica or Wolfram Alpha to work with sequences and series. For example, try Sum[1/k^2,{k,1,Infinity}].

Thursday, November 12

In class, we started discussing series. Roughly speaking, a series is an infinitely long sum. To be precise about what an "infinitely long sum" means, we define series in terms of a sequence of partial sums. Each element in the sequence of partial sums is a finite sum.

The things we discussed in class today fall into Sections 8.2 and 8.3 of the text. You should read the first part of Section 8.2 (up to the subsection entitled "Geometric Series") and the first part of Section 8.3 (through Example 2). We'll cover the other ideas from these Sections in the next few days.

I have not yet assigned problems on series since we have just gotten started. You should continue to work on the Section 8.1 problems (including the two to be submitted tomorrow) and Project #2.

Tuesday, November 10

In class, we looked at a precise way of defining limit of a sequence. This handout has three versions of a definition: an informal version, a precise version, and a compact expression of the precise version. In practice, we use the precise definition of limit to prove a few specific results and general rules. We then use those rules and results to provide rigorous arguments for other specific limits.

In analyzing a sequence, you should distinguish among three levels of reasoning:

• a conjecture based on numerical/graphical evidence
• a conclusion based on informal reasoning
• a conclusion supported by formal reasoning

The appropriate level of reasoning depends on the context. For much of what we do in the future, the second level of reasoning will be appropriate. In working on assigned problems from Section 8.1, you should strive for the third level. Formal reasoning includes

• a proof based directly on the precise definition
• using specfic results and rules (such as given in Theorems 1 and 5 of the text)
• using L'Hopital's rule (by viewing the index variable as representing all real numbers rather than just integers)
• a Sandwich Theorem argument
• a Bounded Monotone Convergence Theorem argument

I've assigned additional problems from Section 8.1 including two problems to be submitted.

Monday, November 9

One theme in the last chunk of material for the course will be the question Is it convergent? (or, equivalently Does it converge?). On Friday, we applied this question to improper integrals. Today, we begin applying it to sequences. Soon, we will apply it to series.

You will want to be very clear on the distinction between sequence and series. Roughly speaking,

• a sequence is an infinitely long ordered list
• a series is an infinitely long ordered sum

Roughly speaking, a sequence is convergent if the elements in the sequence evenually settle down so that there is one value we can reasonably assign as being "at the end of the list". If so, we call that value the limit of the sequence. You can use this rough idea in looking at the problems (particularly 23,27,29,31) I've assigned from Section 8.1. In class tomorrow, we'll develop more precise ways of defining convergent and limit.

Project #2 is due on Tuesday, November 17.

Exam #4 will be on Tuesday December 8 (the last day of class).

Friday, November 6

In class, we used this handout to introduce an extension of definite integral. This idea goes under the heading of improper integrals. We looked at two flavors of improper integrals: those that involve an unbounded domain and those that involve an unbounded range. The text refers to these two flavors as Type I and Type II, respectively. Given an improper integral, we begin with the the central question Is the integral convergent or divergent? If the improper integral is convergent, we can ask about the value.

Extending the area interpretation of definite integral to improper integrals leads to some interesting revelations. We find that it is possible to have an unbounded region that has a finite area. The region under the graph of 1/x² from x=1 to ∞ is an example of this. As you find in Problem 1 from the handout, we can reasonably assign the value of 1 as the area of this unbounded region. In contrast, the region under the graph of 1/x from x=1 to ∞ does not have a finite area as you found in Problem 2.

To avoid muddled thinking about bounded versus unbounded regions and finite versus infinite areas, you should be clear about the distinction between region and area. A region is a set of points (in the plane for our purposes). An area is a number that measures some aspect of a region. (There are other measures of a planar region such as perimeter or diameter.) A region is bounded if it is contained inside some circle centered at the origin. A region is unbounded if there is no circle centered at the origin that contains the region.

The last two problems on the handout introduce the idea of comparison arguments. In some cases, you can determine whether or not a given improper integral is convergent or divergent by comparing it with an improper integral you alreay know about.

Project #2 was distributed in class. It is due on Tuesday, November 17.

Thursday, November 5

Tuesday, November 3

Exam #3 will be on Thursday November 5 from 8:00 to 9:20 am. It will cover material from Sections 7.1 through 7.6 of the text and Euler's method. For the exam, you can bring one page of reference material such as trigonometric identities, basic antiderivatives, and substitution patterns but not examples. This handout has a list of specific objectives.

On the exams from the Fall 2005 section of the course, the most relevant problems are Problems 1 and 2 from Exam #2 and Problems 2 and 3 from Exam #3.

In preparing for this exam, you might find it useful to look at problems outside the context of specific sections. Problems 69-97 of the Practice Exercises on page 499 provide this type of practice. (You can skip Problem 83 since it involves completing the square which we did not practice). On the whole, these problems on relatively challenging. Don't forget basic substition as a tool.

Today (Tuesday), I have office hour from 1:00 to 2:30 and will then be available for appointments until about 5:00. On Wednesday, I'll be available for appointments from 10:00 to 11:30 in the morning and from 2:30 to 3:30 in the afternoon. You can call or email to set up an appointment if you don't want to run the risk of showing up when I've stepped away or already have an appointment.

For reference, here's a list of handouts that have been added or updated recently:

• Euler method problems with solutions added
• Left endpoint approximation problems with solutions added
• Simpson's rule handout
• Objectives for Exam #3.

Monday, November 2

In class, we looked at the algorithm behind the fnInt feature on a TI-82/83/84/85/86. The algorithm differs from a straightforward application of the approximation methods we've developed in several ways:

• It uses a stopping criterion to (generally) acheive a specified tolerance.
• It is an iterative method that is adaptive so that smaller subintervals are used only where needed.
• It is based on an approximation method that is slightly more sophisticated than the methods we have used.

In class (and on a handout I'll post here later), we worked through an example demonstrating the first two aspects of the algorithm. In this example, we used the midpoint approximation rather than the slightly more sophisticated method of the actual algorithm. Here are two main points to take away from our discussion:

• The stopping criterion is a good rule of thumb but not foolproof. The algorithm might produce a result that has an actual error larger than the specified tolerance.
• A smaller tolerance generally requires more iterations and therefore takes longer to complete.

We also saw an example in which the fnInt algorithm returned the error message "TOL NOT MET" indicating that a maximum number of iterations had been completed without the stopping criterion being met.

I do not have problems to assign on these ideas. For the upcoming exam, you will not be responsible for understanding the algorithm. You are responsible for knowing how to use your calculator responsibly.

Exam #3 will be on Thursday November 5 from 8:00 to 9:20 am. It will cover material from Sections 7.1 through 7.6 of the text and Euler's method. For the exam, you can bring one page of notes with things such as trigonometric identities, basic antiderivatives, and substitution patterns but not examples.

Friday, October 30

In class, we looked at the Simpson's rule approximation as an average of two midpoint and one trapezoid approximations. This approach differs from the approach the text uses. As part of this, the meaning of n we have differs from the text's meaning of n in Simpson's rule. This handout has details on our class approach to Simpson's rule and how to reconcile the error bound we used in class with the error bound given at the bottom of page 481. (Short version: 180 times 2⁴ is 2880)

I've added a few problems for Section 7.6.

Project #1 is due on Monday. See below for more comments.

Exam #3 will be on Thursday November 5 from 8:00 to 9:20 am. It will cover material from Sections 7.1 through 7.6 of the text and Euler's method. For the exam, you can bring one page of notes with things such as trigonometric identities, basic antiderivatives, and substitution patterns but not examples.

Thursday, October 29

Your final version of Project #1 is due on Monday, November 2. Here's a handout with a few more style tips. In evaluating your projects, I will look at the following elements (with a rough weighting for each):

• Mathematical content (50%): An excellent paper will be mathematically precise and accurate.
• Organization, flow, clarity, conciseness (25%): An excellent paper will have clear organization that flows smoothly from one idea to the next. Reasoning will be clear and concise.
• Understanding and insight (15%): An excellent paper will reflect careful independent thought that makes clear the author has internalized ideas and has original perspective on the material.
• Technical aspects (10%): An excellent paper will be free of errors in grammar, spelling, and punctuation. All mathematical expressions will be incorporated in the sentence structure. Figures and tables will be produced carefully and placed appropriately with relevant references in the text.

Exam #3 will be on Thursday, November 5. Tomorrow in class, remind me to make a few comments about the exam.

Tuesday, October 27

In class, we began looking at numerical integration. We rely on numerical integation when using the Second Fundamental Theorem of Calculus is difficult or impossible. The general goal for numerical integration is to give a approximate value for a definite integral that is guaranteed to be within a specified tolerance of the exact value (without ever knowing the exact value). So, we need to consider how the compute an approximation that meets the required tolerance.

To guarantee that the tolerance is met, we need a handle on the error. We can't hope to compute an exact value for the error so we settle for an "easy-to-compute" upper bound on the error. To be useful, a bound on the error must be

• no smaller than the actual error
• relatively easy to compute

In class today, we came up with a bound on the error for a left endpoint rectangle approximation using n rectangles. The bound involves the number of rectangles n, the overall endpoints a and b, and the slope of the function's graph as characterized by the derivative of the function. In particular, we need to find an upper bound M on |f′(x)| for all x from a to b. The upper bound we found is

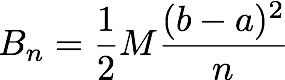
A few more details on this, including an example, are on this handout. The handout also has the assigned problems for today.

Your final version of Project #1 is due on Monday, November 2. Here's a handout with a few more style tips.

Monday, October 26

In class, we looked at how to handle irreducible quadratic factors such as x²+1 in a partial fractions expansion. I've assigned a few additional problems from Section 7.4 that involve this idea.

Friday, October 23

We spent the entire period looking at two problems from Section 7. Problem 49 involves looking at a differential equation called the logistic equation. In addition to the context given in the problem, the logistic equation also shows up in modeling population in an enviroment with limited resources (represented by a carrying capacity). Through lots of hard work, we arrived at a solution to the logistic equation. In class, we got the solution in a particular form. Later, I'll post a handout giving that form and an alternate form that might be easier to understand.

We have one more detail to discuss on partial fractions expansions, namely how to handle irreducible quadratic factors such as x²+1. We'll do that on Monday and then I will post a few additional problems from Section 7.4.

In the meantime, you can work on the problems I've posted for Section 7.5. This section deals with using tables of integrals (such as the one following the index in our text) or technology (such as Mathematica or a TI-89). You can also try on-line tools such as Wolfram Alpha. Note that different tools might give results that look different but are equivalent. For example, compare the result in #88 of the table in our text with what Mathematica or Wolfram Alpha gives for the same integral.

Thursday, October 22

In class, we looked at partial fractions expansions of rational functions. The underlying idea is to have a way of re-expressing a rational function so that we can antidifferentiate using the new expression.

Friday, October 16

We had a computer lab session today so you had opportunity to play with Mathematica. I won't require you to use Mathematica for this course. Mathematica is an option for you to use when appropriate. If you choose to use Mathematica (or similar systems), you'll need to develop judgement about what appropriate means.

Have a great Fall Break.

Thursday, October 15

We continued our survey of integration techniques with a look at trigonometric substitutions.

We also had a quick look at the program Mathematica. At one level, Mathematica is a "super graphing calculator." Mathematica is a commercial product that is available on campus computers. Other similar programs include Maple and Matlab. The Sage project has a goal of producing open-source freely available software with functionality at least as good as available commercial products. We'll go to a computer lab for part of class tomorrow so you can play around with Mathematica yourself. You can also get to some of Mathematica's capabilities through the Wolfram Alpha web site. (Wolfram is the company that produces Mathematica. Wolfram Alpha is a web-based service to provide information and do computations.)

A draft of Project 1 is due tomorrow.

Tuesday, October 13

The main idea for today is using trigonometric identities to rewrite a given integral into a "doable" form. To be successful in this, you need to have access to a variety of trigonometric identities (in your head or on paper) and you need to develop a feel for useful strategies. The latter comes from studying examples and with experience. We looked at a few strategies in class. You'll need to read about others in the text. And, you'll need to practice on lots of problems...

Monday, October 12

Our next goal in the course is to expand our ability to find antiderivatives. We started today with the "anti-product rule" rewritten to give the integration by parts formula.

Friday, October 9

As I mentioned in class, you can submit another attempt of one problem from Exam 2 on Monday. I will grade this second attempt and then replace your original score for that problem with the new score (if it is higher). For this second attempt, you should not consult with anyone else including peers and tutors. You can refer to the text and your class notes. I will return your exams in class on Monday before asking you to submit your second attempt. So, you can prepare work on more than problem and then decide which one to submit once you have your exam back. For reference, here is a copy of Exam 2.

I distribute a handout in class about Project 1 along with general expectations and requirements for projects. A draft of your Project 1 report is due on Friday October 16.

In class, we looked at Euler's method which provides us with a way of numerically approximating a solution of a first-order differential equation. To implement Euler's method, we need a differential equation, an initial condition, and a chosen step size. We computed a few steps for two examples and then looked at spreadsheet results for many more steps. The first example was exponential change and second example used the logistic model. Euler's method is not discussed in our text. This handout has more details for the first example.

Our second example of Euler's method involved the differential equation that comes from the logistic model for population growth. In this model, the per capita rate of change varies linearly with the population. This contrasts with the constant per capita rate of change in our earlier model. (Constant per capita rate of change leads to exponential change.) Later in the semester, we'll be able to find an exact solution to the logistic model differential equation.

Thursday, October 8

Tuesday, October 6

Exam #2 will be on Thursday October 8 from 8:00 am to 9:20 am. It will cover material from Sections 5.6, 6.1, 6.2, 6.3, and 6.5 plus the supplementary material we did on constructing definite integrals for non-geometric quantities (such as total from a density or rate). This handout has a list of specific objectives.

The concept of density is more general than what most of us initially learn as "density is mass divided by volume." We have been using densities over lengths, areas, and volumes that are for a variety of quantities (mass, number, cost, charge, probability,...). This handout has some details and exercises that might help you gain comfort with a more general notion of density.

I've written a handout with a few more problems for additional practice in constructing definite integrals. The context for the second problem will make more sense if you have studied the hydrogen atom in a chemistry or physics course.

In class, someone asked about how well Exam 2 from the last time I taught this course matches with our upcoming exam. On that old Exam 2, Problems 3,4,6, and 7(b) are relevant to what we are currently doing.

Today (Tuesday), I have office hour from 1:00 to 2:30 pm. At 2:30, I have a brief meeting that will last about 15 minutes and then I will be available until at least 4:30 pm. On Wednesday, I currently plan to be available from 10:00 am to 11:30 am in the morning and from 2:30 pm to 4:30 pm in the afternoon.

Some of you came to a study session the evening before Exam 1 and found that to be a productive way to prepare. I'll reserve a room for this to happen again starting at 7:30 pm on Wednesday October 7. I'll post details on the room here later.

Monday, October 5

Today and last Friday, we had a quick look at differential equations. Differential equations are often used in modeling things in the real world. We are only taking a quick look at a very narrow slice of the differential equations world. Math 301 (Differential Equations) gives much more depth in this topic.

Among all differential equations, we will look only at first-order differential equations. And among those, only a few can be solved using separation of variables. After the exam, we'll look at a technique for approximating a solution to a first-order differential equation using what is essentially a Riemann sum.

Exam #2 will be on Thursday October 8 from 8:00 am to 9:20 am. It will cover material from Sections 5.6, 6.1, 6.2, 6.3, and 6.5 plus the supplementary material we did on constructing definite integrals for non-geometric quantities (such as total mass or total number or total future value).

Friday, October 2

We will not cover the material in Section 6.4 of the text. That section deals with constructing definite integrals that give surface area for the surface generated by revolving a curve around an axis.

In class, we first talked about the fact that in constructing a definite integral, we can ignore terms proportional to (Δx)² or higher powers of Δx. These terms contribute nothing to the limit of the Riemann sum. Only terms proportional to Δx itself make a non-zero contribution to the limit of the Riemann sum so it is enough to keep track of these terms.

In class, we also introduced a second topic, namely differential equations. A differential equation is an equation involving an unknown function and one or more of its derivatives. Differential equations are often used in modeling real-world phenomena so we began by thinking about a common kind of modeling situation that involves

• a container (real or conceptual)
• stuff of interest in the container
• a measure of the amount of stuff in the container
• one or more processes that change the amount of stuff in the container

We developed an example in which

• the container is a petri dish
• the stuff of interest is bacteria of a particular species
• the measure of the amount of bacteria is mass of the colony
• the processes that change the amount of bacteria are reproduction and death

Our first simple model was constant reproduction rate and constant death rate. This model predicts linear change in time. Our second simple model was constant per capita reproduction rate and constant per capita death rate. This model predicts exponential change in time.

I've assigned a few problems from Section 6.5. In reading Section 6.5, you can focus on the subsections "Exponential Change" and "Unlimited Population Growth" for now. On Monday, we'll talk about differential equations more generally including the separation of variables solution technique.

Exam #2 will be on Thursday October 8 from 8:00 am to 9:20 am.

Thursday, October 1

In class, we worked through Problem 3(a) from yesterday's handout. The problem involves an entirely non-geometric quantity and so is more abstract for most people. The goal is to construct a definite integral that gives the value V of an account after T years if

• money is deposited into the account on an ongoing basis at a (possibly variable) rate δ

• money in the account earns interest continuously at a rate r.

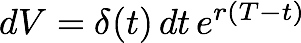
To get the total value, we sum contributions from t=0 to t=T. The total value is thus

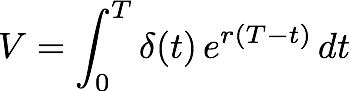
As homework, you should finish off the handout, including Problem 2 to be submitted tomorrow. Here are some notes that might help with Problem 2:

• The density in this problem is not mass per volume. Instead, it is number per area. In the problem, this density is denoted σ.
• In this problem, the density σ can vary with radius. To emphasize this, we could write σ(r) rather than just σ.
• Depending on how you approach the problem, you might wind up needing the area of a circular ring of radius r and thickness dr. One way to get the area is to imagine cutting and unrolling the ring to get a rectangle with dimensions 2πr and dr. The area of the ring is thus dA=2πrdr.

Exam #2 will be on Thursday October 8.

Tuesday, September 29

Today, we turned attention to some examples that involve constructing definite integrals for non-geometric quantities. In class, you worked with others on the first problem from this handout. The first two problems from this handout involve computing the total for some quantity from given density for that quantity. The third problem involves computing a total for a quantity given information about the rate of change in time for that quantity. The new homework assignment is to finish the problems on the handout.

Exam #2 will be on Thursday October 8.

Monday, September 28

In class, we looked at parametric descriptions of curves. For a planar curve, a parametric description in cartesian coordinates consists of giving x and y as functions of an independent variable, often denoted t. In some cases, the parameter t has a geometric meaning. In other cases, t is thought of as time and the parametric description can be thought of as a moving point tracing out the curve in time.

Most graphing calculators have a parametric plot mode. Here is a handout with some details on how to use the parametric plot mode on common TI models (83/84/85/86).

I've assigned additional problems from Section 6.3 that deal with computing arclength for a curve described parametrically.

Friday, September 25

In class, we continued looking at applications that involve building a definite integral to compute some quantity of interest. Our focus today was on computing the length of a curve or arclength.

In Section 6.3, the authors approach the problem of arclength using a parametric description of curves. In class, we worked with non-parametric descriptions of curves. We will talk about parametric descriptions of curves in class on Monday. The problems I've assigned so far from Section 6.3 deal with non-parametric descriptions of curves.

Some time next week, we'll move on to look at some non-geometric applications.

Thursday, September 24

Note that the due date for the problem to be submitted from Section 6.2 has been changed to Monday. There is no new assignment so you have a day to get caught up on things.

In class, we had a quick look at the numerical integration feature available on TI-83/84/85/86 calculators. There are several ways to access that feature. This handout describes both ways.

In class, we also went through a proof of the Second Fundamental Theorem of Calculus. This proof is clean and elegant but provides only limited insight on why FTC2 is true. The proof uses the First Fundamental Theorem of Calculus which explains the ordering of the two theorems in the development we have given. There are other proofs of FTC2 that are more direct and provide more insight but are longer and can be more difficult to understand. In the next day or two, I'll put together an optional handout with details on a direct proof of FTC2.

Tuesday, September 22

Over the last two class sessions, we have built definite integrals to compute volumes of solid regions. Some of these solids regions are solids of revolution that are generated by revolving a planar region around an axis (often the x- or y-axis). For solids of revolution, it is common to slice up the planar region in one of two ways:

• by slicing perpendicular to the axis of rotation
• by slicing parallel to the axis of rotation

For any given situation, we can use either slicing. In some cases, the definite integral we get with one slicing will be easier to build or easy to evaluate than the definite integral we get with the other slicing. In general, it is difficult to tell in advance which slicing will result in easier construction or evaluation. Experience can help but does not provide perfect foresight.

Monday, September 21

Exam #1 was returned in class today. You should carefully review your exam to determine what you need to better understand. As part of this, come ask me questions (including questions to clarify any comments I have written on your exam). As I mentioned in class, I am adjusting the course grading scheme so that your lowest exam score (of the four exams) will count at half the weight of the other exams.

As we continue looking at applications of definite integrals, try to focus on the process of building a definite integral to compute a quantity of interest rather than at general formulas to apply. For example, in Section 6.1, the authors discuss solids of revolution with focus on "the disk method" and "the washer method". For each, there is a nice formula in a box. My preference is to ignore these formulas and instead build an appropriate definite integral (or integrals) for each specific situation one at a time. The main goal for this material is to learn how to build definite integrals rather than learning a list of formulas to be applied in different problems. A secondary goal is continued practice in evaluating definite integrals.

Friday, September 18

We now have the basic story of integration in place and are turning our attention to some applications. Most of these applications involve

• setting up a definite integral (or integrals) equal to a quantity of interest
• evaluating the definite integral(s) to get a numerical value.

In terms of applications, we'll start with examples in which the quantity of interest is geometric such as area, volume, or length. We'll later look at some non-geometric examples.

As homework, you should finish off the problems from the handout we started in class and you should work on the new problems I have assigned from Section 5.6.

Thursday, September 17

Since we had an exam today, no homework for tonight!

Tuesday, September 15

Exam #1 will be Thursday, September 17 from 8:00 to 9:20 am. The exam will cover material from Sections 5.1-5.6 through the subsection "Definite Integrals of Symmetric Functions" that ends on page 363. This handout has a list of specific objectives.

For a definition of definite integral, refer to the handout we used in class. On this exam, you are responsible for the "equal-size subintervals" version on the first page of the handout. You will not be responsible for the more general version on the second page and as given in the textbook.

For the exam, I will give you a few summation formulas and a few derivative formulas (from which you can deduce corresponding antiderivative formulas).

Tutors are available in two locations: the Center for Writing, Learning, and Teaching (Howarth 109) and in Thompson 390. The link at the top of the page will take you to schedules.

I have office hour today (Tuesday) from 1:00 to 2:30. I will also be available most times after that until at least 4:30. Tomorrow (Wednesday), I will be available most of the day except 11:00 am to 2:30 pm. You can stop by to see if I'm free or you can call or email to set up a specific time to meet.

Monday, September 14

In Section 5.6 of the text, there are three distinct topics that are not directly connected with each other: substitution in definite integrals, definite integrals of functions with symmetry (even or odd), and area of regions bounded by curves. We did an example of substitution in definite integrals on Friday in class and a second example today. Today in class, we looked at how we can use symmetry in evaluating definite integrals. We will leave the final topic (area of a region bounded by curves) until after Exam #1.

Exam #1 will be Thursday, September 17 from 8:00 to 9:20 am. (If you have not already replied to my email checking whether or not you are available for the full 80-minute period, please do so as soon as possible.) The exam will cover material from Sections 5.1-5.6 through the subsection "Definite Integrals of Symmetric Functions" that ends on page 363.

Friday, September 11

In class, we looked at antiderivative problems that involve undoing the result of a chain rule. This involves matching the general pattern of a chain rule result. Doing an appropriate substitution helps in recognizing whether or not the general pattern can be matched. Getting comfortable with this process takes a lot of practice so I've assigned many problems from Section 5.5. Some of these are straightforward. Others require a bit of insight or cleverness.

Note that I have not assigned problems to submit from Section 5.5. I will typically do this when an exam is coming up because there will not be time for me to evaluate and return problems before the exam.

Exam #1 will be Thursday, September 17 from 8:00 to 9:20 am. (If you have not already replied to my email checking whether or not you are available for the full 80-minute period, please do so as soon as possible.) The exam will cover material from Sections 5.1-5.6.

Thursday, September 10

In class, we talked about accumulation functions and the First Fundamental Theorem of Calculus. I've put together a handout with some problems on these ideas to replace/supplement the problems in Section 5.4 of the text. The new homework assignment is problems from the handout.

Exam #1 will be Thursday, September 17. I would like to use an 80-minute period for the exam starting at 8:00 am and ending at 9:20 am. I'll soon be sending an email to check if everyone is available to start at that time.

Tuesday, September 8

To the relief of many, we hit the Second Fundamental Theorem of Calculus in class today. Among other things, FTC2 gives us an efficient way to evaluate definite integrals. On Thursday, we'll back up to discuss the First Fundamental Theorem of Calculus (FTC1). FTC1 gives us an important,though less frequently used, computational tool and is used in a proof of FTC2.

For homework, you should finish off problems from the "Practice with FTC2" handout and you should work on the assigned problems from Section 5.4. For a few of the Section 5.4 problems, you'll need to distinguish between signed area and total area. Signed area uses negative values for areas of regions below the horizontal axis. Total area assign positive values to areas of all regions. As an example, the signed area for the sine function sin(x) from x=0 to x=2π is 0 since there are regions of equal size above and below the x-axis. The signed area is given by the definite integral of sin(x) for x=0 to x=2π. On the other hand, the total area is 4. To compute total area, you need to divide the interval into pieces according to where the function is positive and where it is negative. In this case, you need to deal with x=0 to x=π separately from x=π to x=2π.

Friday, September 4

At the end of class, I wrote down a few basic properties of definite integrals that you have seen in your previous calculus experience. A more complete list is given in Table 5.3 on page 336 of the text.

As I mentioned in class, here's a handout with some optional problems exploring integrable and non-integrable functions. This is purely for those who are interested in pursuing ideas that we will not have time to cover fully in class. You are welcome to come talk with me about these problems. If a few people are interested in talking about these problems, we could find time for an informal session outside of class. Let me know if you have an interest.

Thursday, September 3

In class today, we worked through one example of building a Riemann sum and then taking the limit as the number of terms goes to infinity. This is essentially what defines a definite integral. In class tomorrow, we'll write out a complete definition of definite integral.

In the assigned problems from Section 5.2, the first few (1-13 odd) are practice in working with summation notation. Do as many of these (and more) as you need to feel comfortable with using the notation. The last two problems (31, 37) and the problems to be submitted deal with the more important idea of putting together a Riemann sum to estimate an area (or accumulation) and taking a limit to get an exact area (or accumulation).

Building a Riemann sum and then taking the limit as the number of terms goes to infinity generally involves a lot of thinking and computing. You will only have time to do a small handful of examples so you'll need to learn a lot from each example you do. We'll go through at least one more example together in class as we address problems from the Section 5.2 homework.

In big picture, we will soon develop a much more efficient method for evaluating definite integrals that sidesteps the process of building a Riemann sum and taking a limit. We'll use that more efficient method for most of the definite integrals we encounter this semester. However, gettting comfortable with limits of Riemann sums is essentially in understanding the meaning of definite integral. Having a solid grasp on the meaning is necessary in understanding how definite integrals arise in applications and in dealing with those cases in which the more efficient method is not feasible.

After class, one of you pointed out a "typo" I made on the board. Toward the end of the hour, I wrote out the terms in the sum we were building. For the last term, I wrote 125 n³/n³. This should have been 125 n²/n³

Tuesday, September 1

As I mentioned in class, I've put together a handout reviewing some topics from the first semester of the calculus sequence. You might find this useful as a reference. For full details on any specific topic, you'll want to consult the text.

In class, we looked at one example of estimating accumulation given information about rate of change. This corresponds to estimating the area between the graph of a function and the horizontal axis. The assigned problems from Section 5.1 will give you practice in estimating accumulations and areas.

Monday, August 31

To get some idea on expectations for what you should know about material from the first semester of the calculus sequence, here are links to the exams from the last time I taught that course:

Your homework assignment for tonight is to work on Problems 1-23 from Part A of the final exam. You are welcome to look at the other exams but are not required to do so.

Afternoon addition: I've put together a handout reviewing some topics from the first semester of the calculus sequence. You might find this useful as a reference. For full details on any specific topic, you'll want to consult the text.

Handouts

• Calculus review worksheet (Monday, August 31)

Projects

Old exams

You can look at exams from last time I taught Math 181 (which was numbered Math 122 at the time). You can use these to get some idea of how I write exams. Don't assume I am going to write our exams by just making small changes to the old exams. Also note that we were using a different textbook at the time so there are small differences in the ordering of topics, language, and notation. You can use this old exam to prepare for our exam in whatever way you want. I will not provide solutions for the old exam problems.

Useful Class Links

• TI calculator support (including downloadable manuals)

Fun Stuff

• The Mathematical Atlas describes the many fields and subfields of mathematics. The site has numerous links to other interesting and useful sites about mathematics.
• If you are interested in the history of mathematics, a good place to start is the History of Mathematics page at the University of St. Andrews, Scotland.
• Check out the Astronomy Picture of the Day.