

| Monday, December 12 | 10:00-11:30 am | 2:30-3:30 pm |
| Tuesday, December 13 | 10:00-11:30 am | 2:30-3:30 pm |
| Wednesday, December 14 | 10:30-11:30 am | 2:30-3:30 pm |
| Thursday, December 15 | 10:30-11:30 am | 2:00-3:00 pm |
I will have other times that I can be available by appointment. Call or email to set up a time.
| Section/handout | Problems to do | Target date | Comments |
|---|---|---|---|
| Gaussian & error functions | 1,2,3,4 | Tuesday, August 30 | |
| Section 1.1 | 1,2,3,4,5,6,7,9 | Thursday, September 1 | |
| ODE review | 1,2,3,4 | Tuesday, September 6 | |
| Density | 1,2,3,4,5,6 | Thursday, September 8 |
Do as much of this as you need to gain comfort with the idea of non-uniform density. |
| Flux | 1,2,3 | Thursday, September 8 | |
| Section 1.2 | 1,3,4,5,6,7,8 | Monday, September 12 | |
| Section 1.3 | 3,4,5,6,7 | Thursday, September 22 | |
| Laplace equation BVPs | 1-5 | Friday, September 23 | |
| Section 1.7 | 3 | Tuesday, September 27 |
For Problem 3, just try to explain the physical meaning of the relation for a steady-state situation. |
| Section 1.8 | 1,2,3,4 | Thursday, September 29 |
In class on Tuesday, we'll talk briefly about Laplace's equation in polar coordinates. |
| Section 1.5 | 3,4,5 | Thursday, September 29 | |
| Section 2.1 | 1,2,3,4,5 | Tuesday, October 11 | |
| Section 2.4 | 1,2,3,4 | Friday, October 14 |
Problem 3 has been added to this assignment. |
| Section 2.2 | 2,3,5 | Friday, October 21 |
For Problem 2, explicitly evaluate the integral in (2.14) for the given initial velocity (rather than relying on numerical approximation). |
| Section 3.2 | 1,4,5,8 | Friday, October 28 | |
| Section 3.3 | 1,2,3 | Tuesday, November 1 | |
| Section 3.4 | 3,4,6,7,8,9,11 | Monday, November 14 | |
| Section 4.1 | 3 | Tuesday, November 15 | |
| Section 4.2 | 1,2,3,4 | Thursday, November 17 | |
| Section 4.3 | 1,2,3 | Monday, December 5 |
For Problem 1, find the solution as an infinite sum of product solutions. Don't worry about the Poisson integral form. |
| Section 4.5 | 1,2,3 | Monday, December 5 |
Note that this section deals with the heat equation on a disk whereas in class we worked with the wave equation on a disk. |
Topics: vibrations of a circular membrane (general case)
Text: Section 4.5
Mathematica: Visualizing normal modes for a circular membrane (general case)
Tomorrow: There is no tomorrow
Today, we finished off our analysis of normal modes for vibrations of a circular membrane. One way to depict a normal mode is to draw the nodal curves for the mode. We also looked at animations in Mathematica and using the applet available in this collection of math/physics related demonstrations.
Toward the end of class, we briefly discussed isospectral shapes. The spectrum of a shape is the set of frequencies for that shape's normal modes of vibration. In a famous paper entitled "Can one hear the shape of a drum?", Mark Kac asked if two shapes can have the same spectrum. In other words, are there examples of isospectral shapes? The answer turns out to be "Yes, there are isospectral shapes" so one cannot determine a drum shape by sound alone.
Understanding normal modes of vibration is one part of music acoustics. The University of New South Wales has a nice web site with lots of details about music acoustics. You can also go check out Rand Worland's office door (TH 165G, down in the Physics Department) to see the images of vibrating drumheads he creates using holographic techniques.
Exam #7 is due Friday, December 16 by 2 pm. You can turn in your exam anytime you'd like. If you come by when I'm not in, you can either slide your exam under my door or give the exam to our department secretary, Carol Moyer, in TH 414.
Topics: a few more details on vibrations of a circular membrane (rotationally symmetric case); vibrations of a circular membrane (general case)
Text: Section 4.5
Mathematica: Visualizing rotationally symmetric normal modes for a circular membrane
Tomorrow: more on vibrations of a circular membrane (general case)
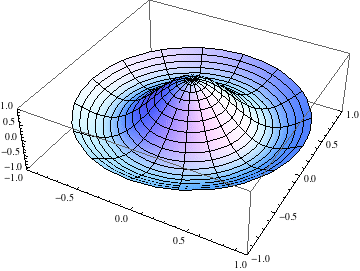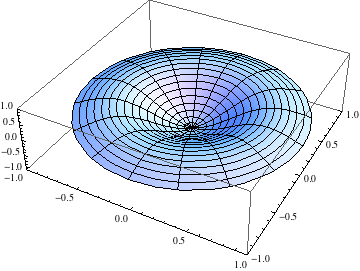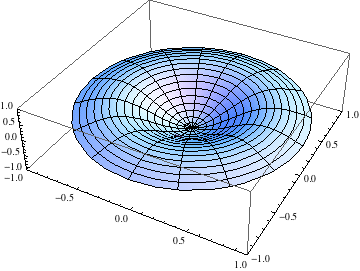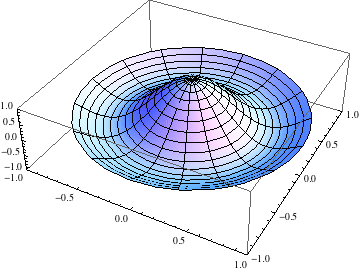
We started with a few more details on our analysis of vibrations of a circular membrane in the rotationally symmetric case. In particular, we look at the nodal curves for a few normal modes. We also talked about the idea of resonance if an external driving force is applied at a frequency that matches a specific normal mode frequency. Finally, we built a general solution as an infinite sum of product (i.e., normal mode) solutions and then applied the initial conditions to get a specific solution. The coefficients in the specific solution are computed as the orthogonal expansion coefficientsf for the initial displacement and initial velocity distributions in terms of the orthogonal set of eigenfunctions. In this case, those orthogonal eigenfunctions are \(J_0(\alpha_n r)\) where \(J_0\) is the Bessel function of the first kind of order \(0\) and \(\alpha_n\) is the \(n^{\text{th}}\) zero of \(J_0\).
We then turned our attention to the general case for vibrations of a circular membrane. While this means dealing with three independent variables, we proceed with the same strategy: start with product solutions and try to separate variables. With three independant variables, we separate in two steps which requires two separation constants and results in two Sturm-Liouville problems. In this case, one of the SL problems was familiar so we could just write down the eigenstuff. The other SL problem involves a second-order ODE that we have not previously solved. That ODE is called Bessel's equation of order m. We'll carry on with this problem tomorrow and get to the point where we can understand the normal modes.
Exam #7 is due Friday, December 16 by 2 pm.
Topics: vibrations of a circular membrane (rotationally symmetric case)
Text: Section 4.5
Mathematica: Visualizing normal modes for a circular membrane
Tomorrow: vibrations of a circular membrane (general case)
Our focus today was analyzing vibrations of a circular membrane. In order to simplify the details, we started with the case of rotationally symmetric vibrations. We set up and an IBVP for the wave equation on a disk using polar coordinates and then assumed no dependence on the angular variable θ. Using product solutions u(r,t)=R(r)T(t) and seaprating variables, we produced an eigenvalue problem for a factor R(r). The second order ODE is not of a type we have previously solved. Fortunately, others have and the solutions are named and well known. Specifically, the general solution is a linear combination of the Bessel function of the first kind of order 0 and the Bessel function of the second kind of order 0. The finiteness boundary condition at r=0 eliminates the second piece. The eigenvalues are then determined by the boundary condition R(A)=0 where A is the radius of the disk. The eigenvalues are the values needed to scale the Bessel function of the first kind of order 0 so that one of its zeroes falls at r=A. With the eigenvalues and eigenfunctions in hand, we solved for T(t) and then put together produce solutions. Each product solution is a normal mode that vibrates at a specific frequency.
Exam #7 is due Friday, December 16 by 2 pm.
Topics: return Exam #6; solving a BVP for Laplace's equation on a disk
Text: Section 4.3
Mathematica: Visualizing solutions for Laplace's equation on a disk
Tomorrow: vibrations of a circular membrane
Today, we stepped through the details of solving our BVP for Laplace's equation on a disk with the temperature distribution specified along the edge. We then visualized the solution for several specific edge distributions.
Topics: solving a BVP for Laplace's equation on a disk
Text: Section 4.3
Tomorrow: solving a BVP for Laplace's equation on a disk
We started class by setting up the full details of a BVP for Laplace's equation on a disk with a prescribed temperature distribution along the edge. The solution will give the state-state temperature everywhere on the disk for that edge temperature distribution. You then started working out the solution using the ideas we've been developing recently. This involves
Before class on Thursday, you should try finishing off the details so that we need only review them quickly in class. As a point of reference, you should find that the eigenvalues are
Note that a regular Sturm-Liouville BVP has just one independent eigenfunction for each eigenvalue. Getting two independent eigenfunctions for most of the eigenvalues does not contradict the Sturm-Liouville theorem we saw earlier because the periodic boundary conditions that arise in this problem do not satisfy the hypotheses for a regular SL problem. One can study general theory for periodic Sturm-Liouville problems but we will not do so.
Topics: another view of our wave equation IBVP solution; a BVP for Laplace's equation on a disk
Text: Sections 4.1, 4.3
Mathematica: Visualizing solutions for a wave equation IBVP
Tomorrow:
We started class by returning to our solution for an wave equation IBVP with Dirichlet boundary conditions. Last week, we saw how to visualize this solution as a sum of right-moving and left-moving pieces. Today, we looked at the same solution as a linear combination of vibrating normal modes. Below is a side-by-side comparison of the two views.
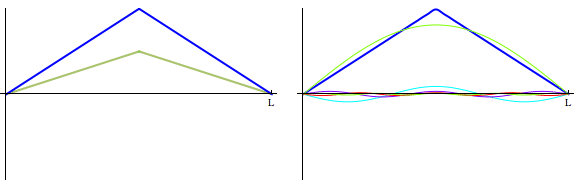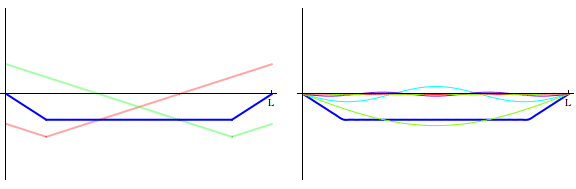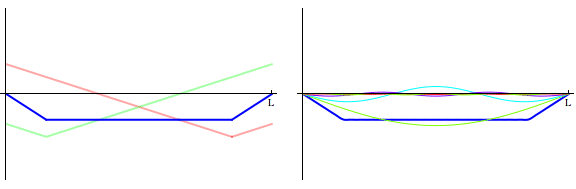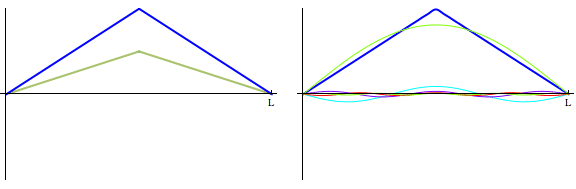
We then turned attention to a BVP for Laplace's equation on a disk. The best way to set up the problem is to use polar coordinates. As a first step, we needed to transform our cartesian form of Laplace's equation to a polar coordinate form. We finished that today so we are set to start in on building a solution tomorrow.
Topics: last problem solution presentation; visualizing solutions for our first IBVP for the wave equation
Text: Sections 4.1 and 4.2
Mathematica: Visualizing solutions for a wave equation IBVP
Tomorrow: TBD
Exam #6 is due Tuesday, November 22 but you can have an extension until tomorrow if needed. If you bring your exam to my office and I'm not in, just slide it under the door.
Have a great break!
Topics: problem solution presentations
Text: Sections 4.1 and 4.2
Tomorrow: problem solution presentations; more on our first IBVP for the wave equation (as time permits)
Exam #6 is due Tuesday, November 22.
Topics: problem solution presentations
Text: Sections 3.4 and 4.1
Mathematica:
Tomorrow: problem solution presentations; more on our first IBVP for the wave equation (as time permits)
Exam #6 is due Tuesday, November 22.
Topics: problem solution presentations
Text: Section 3.4
Tomorrow: problem solution presentations; more on our first IBVP for the wave equation (as time permits)
Exam #6 is due Tuesday, November 22.
Topics: problem solution presentations; distribute Exam #6; an IBVP for the wave equation
Text: Section 4.1
Tomorrow: problem solution presentations; more on our first IBVP for the wave equation (as time permits)
In class, we looked at an IBVP for the wave equation that models vibrations on a string under tension with both ends held fixed. In solving the problem, we used the same approach we've been applying to IBVPs for the heat equation, namely starting with product solutions and then separating variables. In case, we got a familiar BVP for the X(x) factor so we were able to use the results of hard work we had done previously. By the end of class, we had specific product solutions in hand. In the context of the wave equation, these are often called normal modes. Each normal mode is a standing wave vibrating at a specific frequency. When we return to this IBVP, we'll use a linear combination of product solutions to satisfy the initial conditions.
Exam #6 is due Tuesday, November 22.
Topics: return Exam #5; more on the Sturm-Liouville example from Friday
Text: Section 3.4
Mathematica: A Sturm-Liouville example
Tomorrow: problem solution presentations
Today, we reviewed some details from the example of a Sturm-Liouville problem that you worked on Friday. We went a bit further today by finding the first few eigenfunctions. We also computed the first few terms of an orthogonal expansion using these eigenfunction.
Topics: Sturm-Liouville theory
Text: Section 3.4
Tomorrow: an IBVP for the wave equation
We started class by again returning to the X-problem that arose in solving our first example of an IBVP for the heat equation. Without explicitly solving this problem, we were able to use a Rayleigh quotient argument (aka an energy argument) to deduce that all of the eigenvalues are positive.
We then looked at a bit of Sturm-Liouville theory. (Note: The version of these slides that we looked at in class had a typo. The relevant inner product does not have p(x) as a weighting function. This version is corrected.) This theory focuses on deducing properties of eigenvalues and eigenfunctions for second-order ODE boundary-value problems of the type the arise in solving IBVPs for PDEs using separation of variables.
At the end of class, you worked in groups on this example of a Sturm-Liouville problem. In this example, we cannot find an explicit formula for the eigenvalues; the best we can do is approximate the eigenvalues. We can deduce an asymptotic formula that gives a good approximation for larger eigenvalues.
Topics: finishing up with a second IBVP for the heat equation; a taste of Sturm-Liouville theory
Text: Sections 4.2, 3.4
Mathematica: A second heat equation IBVP
Tomorrow: more on Sturm-Liouville theory
Today, we first finished up the heat equation IBVP that you worked on in groups on Tuesday. With boundary conditions for perfect insulation at both ends (i.e., flux is held at zero), we get a different set of eigenfunctions than with the boundary conditions for holding the temperature at zero. So, we end up expanding the initial condition in terms of a basis consisting of 1 and cosines rather than in terms of a basis consisting of sines.
We ended class by returning to the X-problem that arose in solving our first example of an IBVP for the heat equation. Without explicitly solving this problem, we were able to prove that orthogonality for any pair of eigenfunctions corresponding to distinct eigenvalues. This example illustrates one idea of Sturm-Liouville theory. We'll look into this further tomorrow.
Note that I have made the last of the assignments for problem solution presentations. We'll aim to do these next week, although it's possible one or two will spill into the following week.
Topics: a few comments on various norms for R2 (for your cultural benefit); a second IBVP for the heat equation
Text: Section 4.2
Tomorrow: finishing up with a second IBVP for the heat equation; Sturm-Liouville theory
We started class with a few comments on various norms for R2. A norm for a vector space gives us a way of measuring a "size" for each vector. If we specify a norm, we can then define a distance between two vectors as the norm of the difference. In an inner product space, a norm can be specified as the square root of the inner product of a vector with itself.
You then began working out the details of a second IBVP for the heat equation. We'll finish this up on Thursday.
Topics: problem solution presentation; finishing our first IBVP for the heat equation
Text: Section 4.1
Mathematica: Heat equation IBVP
Tomorrow: a second IBVP for the heat equation
Today, we finished off the IBVP for the heat equation that we started last week. This example sets a pattern that we will follow in other problems. Part of this pattern is finding an orthogonal set of functions by solving a BVP for a second-order ODE. (In our first example, this was the X-problem.) Later this week, we'll discuss some general theory behind this part of the process.
Topics: problem solution presentations
Text: Section 4.1
Tomorrow: continuing with an IBVP for the heat equation
On Monday, we'll carry on with solving an IBVP for the heat equation. A crucial step in this will be expressing the initial condition as an orthogonal expansion in terms of the eigenfunctions we found on Tuesday.
Exam #5 is due Monday, November 7.
Topics: problem solution presentations; finding the eigenvalues and eigenfunctions for our heat equation IBVP
Text: Section 4.1
Tomorrow: problem solution presentations; continuing with an IBVP for the heat equation (as time permits)
In the time that remained after problem solution presentations, we worked through the details of finding the eigenvalues and eigenfunctions for our heat equation IBVP. Recall that these come from the BVP for the factor X(x) in our product solutions u(x,t)=X(x)T(t). Our next step in solving the IBVP will be to feed the eigenvalues into the ODE we found for T. The ODE for T is related to the ODE for X by the separation constant λ. The eigenvalues are the special values of λ for which the BVP problem for X has non-trivial solutions. We'll carry on with this solution process tomorrow if time allows and Monday if not.
Exam #5 is due Monday, November 7.
Topics: problem solution presentation; distribute Exam #5 and discuss Gram-Schmidting; continuing with an IBVP for the heat equation
Text: Section 4.1
Tomorrow: problem solution presentations; continuing with an IBVP for the heat equation (as time permits)
After a problem solution presentation and discussing the Gram-Schmidt process for orthogonalizing a linearly independent set of vectors, we returned to the IBVP for the heat equation that we started yesterday. In groups, you worked on the details of the BPV for the function X(x). In particular, you found the general solution to the ODE and then applied the boundary conditions. Doing so carefully requires looking at three cases for the separation constant λ, namely λ>0, λ=0, and λ<0. For most values of λ, only the trivial solution satisfies the boundary conditions. Within the case λ<0, you should find some values of λ that give nontrivial solutions. We'll pull together all of the details on this in class on Thursday. We'll do so at quick pace so you might want to try working out the details yourself before then. Come talk with me if you anticipate being rusty on things like using Euler's formula to extract real-valued solutions to an ODE from a complex-valued solution.
Exam #5 is due Monday, November 7.
Topics: expanding a function in a Fourier sine series and in a Fourier cosine series; starting in on an IBVP for the heat equation
Text: Sections 3.3, 3.1 and 4.1
Mathematica: FSS and FCS example
Tomorrow: continuing with an IBVP for the heat equation
We started class by looking at the expansion of f(x)=x for 0≤x≤1 in two different orthogonal bases for: {sin(kπx)} and {1,cos(kπx)}. We will refer to an orthogonal expansion in the sine basis for L2[0,ℓ] as a Fourier sine series (FSS) and to an orthogonal expansion in the cosine basis for L2[0,ℓ] as a Fourier cosines series. For L2[-ℓ,ℓ], we have seen that {1,cos(kπx),sin(kπx)} is an orthogonal basis. An orthogonal expansion in this basis is called Fourier series (FS). These special cases of orthogonal expansions are named after Joseph Fourier who introduced these as part of his analysis of heat flow. Fourier did his work long before the general framework of vectors spaces, inner products, and orthgonal bases was developed. One of the interesting consequences of Fourier's original work is the way in which it challenged what people thought of as a function. The article "Evolution of the Function Concept: A Brief Survey" by Israel Kleiner (The College Mathematics Journal Vol 20, No. 4 (Sep. 1989), 282-200) gives a nice overview of the historical development of the function idea. [Note: The link is to the JSTOR copy of this article. JSTOR was "experiencing problems" when I put up the link so I'm not sure whether or not it actually works.]
In the second half of class, we began solving an IBVP for the heat equation. Our first step involved a new idea, namely looking for solutions in the form of a product u(x,t)=X(x)T(t). To find conditions on the unknown functions X and T, we ran this form through the heat equation. Using a separation of variables argument, we got an ODE for each of the unknown functions. These ODEs involve the separation constant that we named λ. We then ran the form u(x,t)=X(x)T(t) through the boundary conditions to get two auxillary conditions for X. The combination of the ODE for X and the auxillary conditions is a boundary-value problem (BVP). We will continue with analyzing this BVP tomorrow. One thing we will find is that we get non-trivial solutions only for certain values of the separation constant λ. Those special values of λ are called eigenvalues and the corresponding non-trivial solutions are called eigenfunctions. Sounds like more cool linear algebra ahead!
Topics: orthogonal expansion coefficients minimize distance; mean-square error and mean-square convergence in L2; an orthogonal basis for L2[-ℓ,ℓ] and two for L2[0,ℓ]
Text: Sections 3.1 and 3.2
Mathematica: Mean-square error
Tomorrow: Fourier series: the first orthogonal expansion; back to PDEs
In class, we first showed that the orthogonal expansion coefficients minimize distance between a given vector and a linear combination of orthgonal basis vectors. That is, among all linear combinations of orthogonal basis vectors, the one that minimizes the distance to a given vector is the linear combination using the orthogonal expansion coefficients. In L2, the square of the distance is called the mean-square error. So in L2, the orthogonal expansion coefficients minimize the mean-square error.
We ended class by listing some orthogonal bases for various L2 spaces. In particular, we listed two orthogonal bases for L2[0,ℓ], one with sine functions and the other with cosine functions. As part of your homework for the weekend, you should compute the orthogonal expansion of f(x)=x for 0≤x≤1 using each of those bases. That is, you should compute the expansion of f(x)=x using the sine basis and compute the expansion of f(x)=x using the cosine basis.
Next week, we will see that in the process of solving a PDE problem on a bounded interval, we will need to expand an initial condition in terms of an orthogonal basis. The PDE and the boundary conditions will dictate which basis we need to use.
Topics: another example of orthogonal expansion in L2; inner product, norm, and distance; orthogonal expansions and minimizing distance
Text: Sections 3.1 and 3.2
Mathematica: One more orthogonal expansion example
Tomorrow: more on orthogonal expansions and minimizing distance
Today, we started with another example of expanding a function, specifically the exponential function, in L2[-π,π] using the basis {1}∪{cos(kx)}∪{sin(kx)}. We then turned attention to the natural way of measuring distance between vectors in an inner product space. Using the inner product, we first define norm (or magnitude or, in a geometric setting, length) of a vector v as ||v||=√⟨v,v⟩. We then define the distance between two vectors v and w as the norm of the difference v-w. That is, we define d(v,w)=||v-w||. By looking at an example in R3 and the beginning of an example in L2, we saw a relationship between minimizing distance and computing an orthogonal expansion. We'll explore this further tomorrow.
Topics: convergence of orthogonal expansions in L2
Text: Sections 3.1 and 3.2
Mathematica: More orthogonal expansions
Tomorrow: more on orthogonal expansions in L2
Our immediate goal is to understand orthogonal expansions as a tool we will be using in the process of solving PDEs on bounded intervals. The setting for an orthogonal expansion is a vector space V with an inner product ⟨ , ⟩. In many contexts, it is convenient (or necessary) to work with a basis for the vector space. In an inner product space, the best type of basis is an orthogonal basis. In an inner product space, two elements are orthogonal if their inner product is zero. A set is orthogonal if each pair of elements in the set is orthogonal. An orthognal basis for an inner product space is a basis that is orthogonal (duh!).
For our purposes in solving PDEs, we will work with the vector space L2[a,b] consisting of "nice" functions with domain [a,b]. The vector space L2[a,b] is infinite dimensional. For infinite dimensional vector spaces, there are subtle issues in determining whether or not a given set is a basis. Even with a basis in hand, there are additional convergence issues in expanding a vector in terms of a basis.
In class, we explored a few examples of convergence for orthogonal expansions in L2. The context is that we start with a function f and then compute the coefficients ak so that we can construct the orthogonal expansion OE, which is a function itself. By looking at examples, we saw that an orthogonal expansion OE does not necessarily converge to the function f for all x in the relevant domain. In particular, the orthogonal expansion does not necessarily converge pointwise to f.
Tomorrow, we will look at a different notion of convergence in which the difference between OE(x) and f(x) is measured using the norm given by our L2 inner product. This type of convergence is called normwise convergence in a general context. In the specific context of our L2 inner product, it can also be called mean-square convergence (because the distance in this case is essentially averaging the square of the difference between two functions).
Exam #4 is due by 5 pm on Wednesday, October 26. If you choose to turn in your exam on Wednesday, you can bring it to my office (and slide it under the door if I'm not in) or leave it with Carol Moyer (our department secretary) in TH 414.
Topics: orthogonal expansions
Text: Sections 3.1 and 3.2
Mathematica: Orthogonal expansions
Tomorrow: convergence of orthogonal expansions in L2
In class, we looked at an example of orthogonal expansion in R3. We started with a basis this is orthogonal with respect to the standard inner product (i.e., the dot product) for R3. We then looked at expanding another vector as a linear combination of the basis vectors. Finding the expansion coefficients for a general basis requires solving a system of equations. For an orthogonal basis, we can easily compute the expansion coefficients using the inner product.
We next looked at generalizing from R3 to a vector space of "nice" functions with domain [-π,π]. The specific vector space with which we will work is called L2(-π,π). (We'll get more details on this vector space later.) For this vector space, the standard inner product is an integral of the product of functions f and g. With respect to that inner product, the set {sin(kx)} is orthogonal. We looked at an example of expanding another function in the vector space as a linear combination of these orthogonal functions. We'll look at other examples tomorrow.
I made a bogus argument in class. When we were looking at orthogonality of sin(x) and sin(2x), I used a symmetry argument to conclude that the relevant integral is zero. Each of the functions sin(x) and sin(2x) is odd. The product of two odd functions is even (rather than odd as I stated in class). So, we cannot conclude that the integral is zero by a symmetry argument. At best, we can use the even symmetry to write the integral from -π to π as twice the integral from 0 to π . To show that the integral is indeed equal to zero, we actually have to do some work. We'll take care of that in class tomorrow. Even though my argument was bogus (for which I plead temporary insanity), the conclusion is true: sin(mx) and sin(nx) are orthogonal for any integers m and n with m ≠ n.
Exam #4 is due by 5 pm on Wednesday, October 26. If you choose to turn in your exam on Wednesday, you can bring it to my office (and slide it under the door if I'm not in) or leave it with Carol Moyer (our department secretary) in TH 414.
Topics: the heat equation on a bounded interval
Text: Sections 3.1 and 3.2
Tomorrow: orthogonal expansions
Today, we turned our attention to an IBVP for the heat equation on a bounded interval. Our first thought was to relate this new problem to an old problem, namely the Cauchy problem for the heat equation. So, we began thinking about how to extend the intial condition for the given interval 0 < x < L to an initial condition for all x in such a way that the given boundary conditions would be satisfied by the evolving solution. This seemed to be a complicated task so we abandoned ship. Instead, we will develop a new approach. Part of this new approach will require us to develop some new mathematical tools. As an introduction to this, we went to the computer lab where you did some work in Mathematica to experiment with approximating a given function using a linear combination of sine functions. As homework, you should finish up this experimentation (from the handout) and bring your coefficient values to class on Monday.
We are going to skip over the rest of Chapter 2 for now. If time permits, we'll circle back toward the end of the semester to talk about integral transform approaches to solving PDEs on unbounded domains.
Note added Saturday Ocotber 22: In talking with a few of you this week, I realized that you might find it useful to have some written details on the delta function that we have defined in class. So, I've written this handout summarizing what we've discussed in class. The handout also includes details on how to evaluate an integral that involves the delta function. Please let me know if you spot errors/typos or if you have questions on the content.
Exam #4 is due on Tuesdayy, October 25.
Topics: return Exam #3; density plots; the Cauchy problem for the wave equation
Text: Sections 2.1, 2.4
Mathematica: Visualizing the fundamental solution for the heat equation in two-dimensions
Mathematica: Visualizing wave equation Cauchy problem solutions
Tomorrow: the heat equation on a bounded interval
Today, we looked at the Cauchy problem for the wave equation. The Cauchy problem consists of the wave equation \(u_{tt}=c^2 u_{xx}\) for \(-\infty\lt x\lt \infty\) and \(t>0\) together with an initial displacement distribution \(u(x,0)=u_0(x)\) and an initial velocity distribution \(u_t(x,0)=v_0(x)\) for \(-\infty\lt x\lt \infty\). Finding the specific solution for this problem is much easier than what we went through to find the specific solution for the heat equation Cauchy problem because we already have the general solution for the wave equation hand, namely \( u(x,t)=F(x-ct)+G(x+ct) \) for arbitrary functions \(F\) and \(G\). We need only apply the initial conditions to determine \(F\) and \(G\) in terms of \(u_0\) and \(v_0\). Doing so gave us the specific solution in the form \[ u(x,t)=\frac{1}{2}u_0(x-ct)+\frac{1}{2}u_0(x+ct) +\frac{1}{2c}\int_{x-ct}^{x+ct}v_0(z)\,dz. \]
I have assigned problems from Section 2.2 and added one problem to the assignment from Section 2.4.
Exam #4 is due on Tuesday, October 25.
Topics: one more problem solution presentation; debriefing on some ideas from recent problem solution presentations
Text: Sections 2.1, 2.4
Mathematica: Visualizing solutions to Section 2.1 #1
Mathematica: Visualizing the fundamental solution for the heat equation in two-dimensions
Tomorrow: the Cauchy problem for the wave equation
After a homework solution presentation, we looked back at some of the homework solution presentations from recent days with some extensions and visualizations.
When we return from break, we'll look at the Cauchy problem for the wave equation. Finding the specific solution for this problem will be much easier than what we went through to find the specific solution for the heat equation Cauchy problem because we already have the general solution for the wave equation hand, namely \( u(x,t)=F(x-ct)+G(x+ct) \) for arbitrary functions \(F\) and \(G\).
Toward the end of break, I'll post the next exam here. In the meantimem, you can look at the assigned problems from Section 2.4.
Have a great break!
Topics: problem solution presentations
Text: Sections 2.1, 2.4
Tomorrow: one more problem solution presentation; debriefing on some ideas from recent problem solution presentations; the Cauchy problem for the wave equation
I've assigned a few problems from Section 2.4 of the text that deal with IBVPs for the heat equation on a half-line.
We've skipped ahead to Section 2.4 in the text. We'll soon come back to the ideas in Sections 2.2 and 2.3.
Topics: problem solution presentations; IBVPs for the heat equation on the half-line
Text: Sections 2.1, 2.4
Mathematica: A solution for an IBVP for heat equation on the half-line
Tomorrow: problem solution presentations
Today, we solved the general IBVP for the heat equation on the half-line with boundary condition u(0,t)=0 for t > 0. We did this building the odd extension of the initial condition so we have a new initial condition defined for all x. This gives us a Cauchy problem for which we already have the solution. Using the odd extension insures that the boundary condition is satisfied.
In attempting to animate the half-line solution for a specific initial condition, I made a mistake with the Mathematica code. So, the animation we saw at the very end was actual for a Gaussian initial condition rather than for the function \(\displaystyle u_0(x)=\frac{\sin x}{x}\) suggested by Lukas. Animating the solution for that initial condition involves some technical issues that we can talk about on Thursday or Friday.
We've skipped ahead to Section 2.4 in the text. We'll soon come back to the ideas in Sections 2.2 and 2.3.
Topics: working with our solution for the general heat equation Cauchy problem
Text: Section 2.1
Mathematica: A solution for a heat equation Cauchy problem
Tomorrow: problem solution presentations
Today, we reviewed the somewhat lengthy process we undertook to arrive at the specific solution for a general heat equation Cauchy problem in one spatial dimension. For the initial condition \(u(x,0)=u_0(x)\), the specific solution is \[ u(x,t)=\int_{-\infty}^\infty u_0(y)G(x-y,t)\,dy \qquad\textrm{where}\qquad G(x,t)=\frac{1}{\sqrt{4\pi k t}}e^{-x^2/4kt}. \] We can interpret this as a continuum "linear combination" of time-evolving Gaussians. To get some feel for this solution, we picked an explicit initial condition and then worked hard to evaluate the integral. We were able to get a nice expression for the specific solution in this case. Being able to do so is rare. We'll see a few more examples in the problem solution presentations tomorrow.
Topics: building a solution for the general heat equation Cauchy problem
Text: Section 2.1
Tomorrow: working with our solution for the general heat equation Cauchy problem
In class, we derived the solution for a general heat equation Cauchy problem. The full derivation has taken several days. Here's an outline of the steps:
At the end of class today, we made a quick argument for this last step. On Monday, we'll go through that argument again with a bit more detail. We'll also work with this specific solution to get a better feel for what it all means.
Exam #3 is due on Monday, October 10.
Topics: using dimensional analysis to solve a specific Cauchy problem for the heat equation
Text: Section 2.1
Mathematica: Animating a heat equation solution
Tomorrow: building a solution for the general heat equation Cauchy problem
In class, we solved a specific Cauchy problem for the heat equation with the initial condition consisting of a step function (0 for \(x<0\) and \(w_0\) for \(x>0\)). Our strategy was to use dimensional analysis to show that the solution must be in the form of a relation between two dimensional quantities \(\pi_1\) and \(\pi_2\). We expressed that relation as \(\pi_1=f(\pi_2)\) for some unknown function \(f\). To determine \(f\), we substituted back into the original PDE and found a condition (specifically, an ODE) on \(f\). We then solved the ODE and applied the initial condition. One issue we encountered is that our general solution to the ODE is not defined for \(t=0\). So, we did the next best thing: we set the limit of the general solution as \(t\to 0^{+}\) equal to the given initial condition and used this to determine specific values for the constants that appear in the general solution.
Tomorrow, we will build on what we did today to eventually get a specific solution for a general heat equation Cauchy problem.
Exam #3 is due on Monday, October 10.
Topics: return Exam #2; more on dimensional analysis; first steps of solving a specific Cauchy problem for the heat equation
Text: Section 2.1
Mathematica: Row reducing and rank in Mathematica
Tomorrow: using dimensional analysis to solve a specific Cauchy problem for the heat equation
Today, we looked at two examples of using dimensional analysis to reformulate a relationship among physical quantities as an equivalent relationship among dimensionless variables formed as combinations of the original variables. We then started in on applying this idea to a specific Cauchy problem for the heat equation in which the initial distribution is a step function. We will use dimensional analysis to generate a guess (or ansatz) for the form of the solution. This guess has some freedom (in this case, an unknown function of one variable). Substituting the guess into the PDE generates a condition on the free part (in this case, an ODE for the unknown function of one variable). Solving the condition gives us a solution to the original problem.
Exam #3 is due on Monday, October 10.
Topics: problem solution presentation (Aimee); a few more comments on classifying second-order linear PDEs in two independent variables; the Cauchy problem for the heat equation; a first look at dimensional analysis
Text: Sections 1.9 and 2.1
Tomorrow: more on dimensional analysis; first steps of solving a specific Cauchy problem for the heat equation
Section 1.9 looks at the classification of second-order linear PDEs (as hyperbolic, parabolic, or elliptic) and at finding characterisitic coordinates that transform the second-order terms of the PDE to a standard form. One of the big ideas in all of this is that it is enough to understand how to analyze a prototype for each of the categories since other equations can be related to one of the prototypes. So, for the remainer of the course, we will focus on the prototypes:
Focussing on these three is much less limited than it might initially appear.
Our next major goal for the course is to analyze the Cauchy problem for the heat equation in one spatial variable. The Cauchy problem consists of the heat equation \(u_{t}=k u_{xx}\) for \(-\infty\lt x\lt\infty\), \(t\geq 0\) together with an initial condition \(u(x,0)=u_{0}(x)\) for \(-\infty\lt x\lt\infty\). This is a pure initial value problem since the unbounded domain in x requires no boundary conditions.
Our approach to analyzing the Cauchy problem for the heat equation will start with a sidenote on dimensional analysis. We saw one quick example today and will go through one or two others a bit more systematically tomorrow.
Topics: problem solution presentations (Matthew, Amy, Sam, Katie R)
Text: Section 1.9
Tomorrow: problem solution presentation (Aimee); a few more comments on classifying second-order linear PDEs in two independent variables
Topics: problem solution presentations (Lizzi, Caitlin); animating a wave equation solution; classifying second-order linear PDEs in two independent variables
Text: Section 1.9
Mathematica: Animating a wave equation solution
Tomorrow: problem solution presentations (Matthew, Amy, Sam, Katie R, Aimee)
One theme from today's problem solution presentations is that the steady-state condition corresponds to uniform flux. If the flux is that same at all points, then at each point heat energy density does not pile up or spread out. In one dimension, if the thermal conductivity (a.k.a. the diffusivity or diffusion constant) is uniform, then the steady-state distribution is linear. If the thermal conductivity/diffusivity/diffusion constant is not uniform, then the steady-state distribution is not linear.
After a quick look at animating a wave equation solution, we turned to the issue of classifying second-order linear PDEs in two independent variables. The conclusion of the story is that we can sort these PDEs into three categories: elliptic, parabolic, and hyperbolic. Laplace's equation is the prototypical elliptic equation, the heat/diffusion equation is the prototypical parabolic equation, and the wave equation is the prototypical hyperbolic equation. The naming of these three categories is by analogy with a classification of second-degree algebraic equations in two variables (a.k.a. quadratic equations). The graph for a quadratic equation is either an ellipse, a parabola, or a hyperbola. In class, we had a very rapid overview of how quadratic equations are classified. You can read more details on this optional handout. The classification makes beautiful use of many ideas from linear algebra. Section 1.9 gives the corresponding details for second-order linear PDEs (without directly using linear algebra tools). We will not cover these ideas in detail and I will not assign problems from Section 1.9. We will talk briefly on Monday about how classifying second-order linear PDEs uses many of the same ideas as classifying second-order algebraic equations.
Topics: Laplace's equation in polar coordinates; motivating the wave equation; solving the wave equation
Text: Sections 1.8 and 1.5
Mathematica: Solution and plots for a Laplace BVP
Tomorrow: classifying second-order linear PDEs in two independent variables
In class, we looked at modeling vibrations on a string under tension as a way of getting to the wave equation. We then analyzed the wave equation using characteristic coordinates. By transforming to appropriate characteristic coordinates, we were able to put the wave equation in a form that we could integrate twice to arrive at a general solution in the form u(x,t)=F(x-ct)+G(x+ct). for arbitrary function F and G. This general solution has a simple interpretation: For t=0, we start with u(x,0)=F(x)+G(x). For t>0, the solution corresponds to F translating to the right in x and G translating to the left in x, both at speed c as t increases.
You can find a more detailed derivation of the wave equation in the first part of Section 1.5. The second part of Section 1.5 shows how the wave equation arises in modeling sound waves under certain conditions. Those of you majoring in physics should consider reading this part of Section 1.5. The starting point is to look at the fundamental conservation law as applied to both mass and momentum.
I have assigned problems for the next group of solution presentations.
Topics: comments on recent problems; the "perfect insulation" boundary condition; general properties of Laplace equation solutions
Text: Sections 1.3, 1.7, and 1.8
Tomorrow: Laplace's equation in polar coordinates; the wave equation
We started class with some comments following up on problem solutions from last Friday. We then look at the "perfect insulation" boundary condition. This boundary condition can be stated as "the component of the flux normal to the boundary must be zero" which, for diffusion, translates into a statement about the normal component of the density gradient being zero along the boundary. This implies that a steady-state solution has level curves that are perpendicular to any boundary on which we assume perfect insulation.
We then formulated a quick and dirty version of the maximum principle for Laplace equation solutions. You should read the more precise version given in Section 1.8 of the text. You should also read about the mean-value property of Laplace equation solutions.
Topics: problem solution presentations
Text: Sections 1.3, 1.7, and 1.8
Tomorrow: more on Laplace's equation
One theme that emerged in the problem solutions we saw today was the idea of looking at how a solution depends on one or more parameters (or on some combination of parameters such as \(\sqrt{a/k}\) in 1.3 #6). Looking at extreme values of a parameter or combination of parameters (often \(0\) and the limit at \(\infty\)) can be good consistency checks on the solution. These extremes generally correspond to turning off a process or having one process dominate over the others in the model. For example, in 1.3 #6, look at the case \(\sqrt{a/k}=0\) corresponds to turning off the heat loss process (so perfect insulation on the lateral boundary of the bar) while the case \(\sqrt{a/k}\to\infty\) corresponds to turning off the diffusion process.
Exam #2 is due on Monday, September 26. In thinking about using your general solution to explicitly show that the amount of stuff is conserved, you should assume that there is initially a finite amount of stuff.
Topics: problem solution presentation; boundary value problems for Laplace's equation
Text: Sections 1.3, 1.7, and 1.8
Tomorrow: problem solution presentations; more on Laplace's equation
Today, you worked in groups on these problems that involve setting up and developing some intuition for boundary-value problems for Laplace's equation. The boundary conditions will come in the forms described in Section 1.3 (for one spatial dimension) and Section 1.7 (for more than one spatial dimension). One specific condition is that perfect insulation corresponds to having the component of the flux normal to the boundary be zero.
Problems 4 and 5 on the handout involve a circular domain. For this, polar coordinates are useful. You should read the relevant parts of Section 1.8 to see the form of Laplace's equation in polar coordinates.
Section 1.8 also discusses two general properties of Laplace equation solutions: the mean-value property and the maximum principle. We'll talk about these in class sometime in the next few days.
As you have noticed, we have skipped over a few sections. We will circle back next week to talk about the main ideas in Section 1.5. You are welcome to read Sections 1.4 and 1.6 as your interests dictate. Section 1.4 develops some basic PDE models in the context of population modeling. Many of the ideas in this section are versions of what we have done specific to thinking about how the spatial distribution of a population evolves in time. This section also includes a random-walk derivation of the diffusion equation. Section 1.4 provides a nice review and extension of many ideas we have discussed and is well worth reading. Section 1.6 describes the central equation of quantum mechanics, namely Schrödinger's equation.
Exam #2 is due on Monday, September 26. In thinking about using your general solution to explicitly show that the amount of stuff is conserved, you should assume that there is initially a finite amount of stuff.
Topics: boundary conditions for heat flow problems; diffusion in more than one dimension; Laplace's equation
Text: Sections 1.3, 1.7, and 1.8
Tomorrow: problem solution presentations (maybe); more on Laplace's equation; the wave equation
At the beginning of class, we set the order for the second round of problem solution presentations. I'll get this information up later today and send out problem assignments to the first few people on the list.
We then looked at a variety of boundary conditions for heat flow problems in one spatial dimension. At an endpoint, we can control the heat energy density (that is, control the temperature), the flux, or some combination of the two. Mathematically, these translate into prescribing the value of the function at the endpoint, prescribing the value of the spatial derivative of the function at the endpoint, or prescribing the value of some linear combination of the two at the endpoint.
We next moved on to talk very briefly about diffusion in more than one spatial dimension. Doing so brings in the idea of flux as a vector along with some ideas from vector calculus such as gradient and divergence. If we want go back a step further to derive the fundamental conservation law for more than one spatial variable, we would also need to recall the divergence theorem (a.k.a Gauss's theorem in the physics world). You may have talked about divergence and the divergence theorem only briefly at the end of your multivariate calculus course. At the end of the set-up, we used cartesian coordinates to get an expression that should seem like a natural generalization. Specifically, the expression uxx in the heat equation for one spatial dimension generalizes to uxx+uyy in the heat equation for two spatial variables. In this more general setting, we have u(x,y,t) generalizing u(x,t).
Our initial interest in the heat equation for two spatial variables will be in steady-state solutions. These are given by Laplace's equation uxx+uyy=0. Laplaces' equation also shows up in modeling other physical phenomena such as electrostatic potentials. We'll focus on interpreting Laplace's equation as the condition for steady-state temperature distributions since we can have some basic intuition for that setting.
Exam #2 is due on Monday, September 26.
Topics: diffusion
Text: Section 1.3
Tomorrow: boundary conditions for heat flow problems; diffusion in more than one dimension; Laplace's equation
Diffusion is a general process in which stuff moves from regions of higher density toward regions of lower density. We developed a simple relationship between flux and density as a model for diffusion. The relationship is that flux is proportional to the opposite of the rate of change in density (with respect to position). Using this relationship in the fundamental conservation law gives us the diffusion equation.
Heat energy flows by diffusion and so provide a nice context. Thinking about the diffusion equation in the context of heat energy flow provides a nice setting for interpreting various boundary conditions. In many cases, we'll think explicitly about temperature since temperature is proportional to heat energy density for a given material. Temperature is more intuitive than heat energy density. In the example we set up today, we used a boundary condition for each end of a finite-length rod that prescribes the temparature at that end. Tomorrow, we'll look at other boundary conditions that arise naturally in setting up heat energy flow models.
Topics: return Exam #1; mathematical software systems
Tomorrow: diffusion
Today, we looking at some mathematical software systems. In general, a mathematical software system provides functionality for symbolic, numeric, and graphic manipulations. We looked briefly at Sage and Mathematica.
Sage is an open-source, freely-available system. You can use Sage either by downloading and installing a copy on your own machine or by accessing a Sage server through a web browser. One option is the public Sage server at the University of Washington. If you are on campus, another option is the Puget Sound Sage server. To access each one, you will need to create an account.
Mathematica is a commercial system that comes at a price. As a student, that price is included in your tuition. You will find Mathematica on many university owned computers (and perhaps all now that it is being served through the vDesk system). You can also get to Mathematica while off-campus using Puget Sounds' vDesk virtual desktop system.
You can access many features of Mathematica using WolframAlpha. Wolfram is the company that produces Mathematica. WolframAlpha is web-based "computational knowledge engine". Among other things, WolframAlpha will do numeric, symbolic, and graphic manipulations. You can enter commands in natural language (which can is ambiguous and can be interpreted in some way other than what you intend) or using Mathematica syntax (which is unambiguous but requires understanding of the syntax).
Topics: last solution presentations for Section 1.2
Text: Section 1.2
Mathematica: Visualizations for Section 1.2 #5 and #7
Tomorrow: diffusion or computer lab session
In the problem solutions we had today, we saw several uses of characteristic coordinates to solve first-order linear PDEs. Each of the problems included finding a general solution and then applying an initial condition to find a specific solution. For Section 1.2 #7, we are given an explicit initial condition so the specific solution is very concrete. For the two parts of Section 1.2 #5, the initial condition is named but not given explicitly. As a result, the specific solution does not seem very specific. For both parts, the general solution gives \(u(x,t)\) in terms of an arbitrary function while the specific solution gives \(u(x,t)\) in terms of the given (or named) initial condition. More generally, a specific solution will give \(u(x,t)\) in terms of some combination of initial conditions and boundary conditions (as we saw, for example, in Section 1.2 #6).
In all three cases, we can understand and visualize the specific solution in terms of time-dependent scalings and shiftings of the initial condition. You should make routinely attempt this type of understanding whenever you come across a solution. First do this without the aid of computing technology. You can then turn to computing technology for confirmation of your understanding.
Topics: problem solution presentations for Section 1.2
Text: Section 1.2
Mathematica: Visualizations for Section 1.2 #6
Tomorrow:
In looking at solutions to PDE problems, we will often find a solution and then spend considerable time working to understand that solution. Section 1.2 #6 provides a good example of this. In your own work on solving problems for homework and exams, you should go beyond symbolic manipulations to arrive at a formula for the solution to trying to understand that solution either using visualizations (such as plot and animations) or in terms of a real-world image (such as dye in a fluid).
Topics: more on characteristic coordinates
Text: Section 1.2
Tomorrow: problem solution presentations for Section 1.2
We started class working in groups on these problems with the goal of getting some feel for the geometry of characteristics coordinates. Recall that the basic idea is to find new coordinates \(r\) and \(s\) in terms of the original coordinates \(x\) and \(t\) so that the expression \(u_t+cu_x\) simplifies to \(U_s\). In the new coordinates, the PDE \(u_t+cu_x+c_xu=f\) reduces to an ODE of the form \(U_s+aU=F\) for each value of \(r\). So, this ODE tells how \(U\) changes with respect to \(s\) along a curve of constant \(r\). Solving the ODE and converting back to the original variables gives us a solution for \(u\) in terms of \(x\) and \(t\).
Finding characteristic coordinates is relatively straightforward if \(c\) does not depend on \(x\). To handle cases in which \(c\) does depend on \(x\), we argued that along each constant \(r\) curve, we must have \(dx=c\,dt\). To find a choice of \(r\), we can separate variables, integrate, and then find a combination of \(x\) and \(t\) that is constant. This gives us a choice of \(r\). Note that the choice is not unique since there are many combinations of \(x\) and \(t\) that are constant.
Topics: problem solution presentations; characteristic coordinates and solving the advection equation
Text: Section 1.2
Tomorrow: more on characteristic coordinates
Today, we looked at the idea of characteristic coordinates as an approach to solving advection equations. The basic idea is to find new coordinates \(r\) and \(s\) in terms of the original coordinates \(x\) and \(t\) so that the expression \(u_t+cu_x\) simplifies to \(U_s\). There is a lot of freedom in finding suitable characteristic coordinates. We made a set of choices that ends with \(s=t\) and \(r\) satisfying the conditions \(r_x=1\) and \(r_t=c\). If \(c\) is constant, these conditions result in \(r=x-ct\). If \(c\) is not constant, we have more work to do. If \(c\) depends only in \(t\), we can integrate \(r_t=c\). If \(c\) depends on \(x\), the situation is less obvious. We'll deal with that case on Monday. In the meantime, you can work on the additional problems I've assigned from Section 1.2. You can hold off on Problem 5 until after class on Monday since that problem involves cases with \(c\) depending on \(x\).
Exam #1 is due on Monday, September 12.
Topics: problem solution presentations for ODE review; developing some intuition for the fundamental conservation law; advection
Text: Section 1.2
Tomorrow: problem solution presentations; more on advection; solving the advection equation
The fundamental conservation law relates the time rate of change in density to the spatial rate of change in flux. Using a very simplistic view, we tried to make some intuitive sense of this relationship by thinking about how the density at a point changes in time (increasing, staying constant, or decreasing) for various scenarios in which flux changes with position (increasing, staying uniform, or decreasing). We then had a quick look at the advection assumption relating flux to density. Using the advection assumption in the fundamental conservation law gives us a PDE for the density. Tomorrow, we'll look at how to analyze that PDE.
We did not get far enough today to justify assigning more problems from Section 1.2. I'll do that after class tomorrow.
Exam #1 is due on Monday, September 12.
Topics: density, flux, and conservation
Text: Section 1.2
Tomorrow: problem solution presentations for ODE review; developing some intuition for the fundamental conservation law; advection
Today, we derived the fundamental conservation law. This involves some basic accounting that relates total rate of change for the amount of stuff in a generic piece to the sum of three contributions, two accounting for change by flow at the ends of the piece and the other accounting for change by some (generic) creation/destruction process. With some mathematical moves, we can go from an integral version to a differential version so that we can understand the relevant relations on a point-by-point basis. What we discussed in class is covered in the first few pages of Section 1.2. On Thursday, we'll look at two specific models of how flux is related to density that correspond to flow by advection and flow by diffusion.
To better understand the fundamental conservation law, you'll want to develop good intuition for density and flux. To help with this, I've put together two handouts. The first handout on density starts with some trivial exercises about computing total from density when the density is uniform. It then moves on to the non-trivial situation of computing total from density with non-uniform distributions. The second handout gives some details on flux and includes a few problems. The first two are straightforward calculations while the third involves a bit more thinking.
I have assigned a few problems from Section 1.2. I'll assign more after class on Thursday. Note that I have also made some more problem solution presentation assignments.
Exam #1 is due on Monday, September 12.
Topics: problem solution presentation (Katie R); comments on Section 1.1 problems
Text: Section 1.1
Mathematica: Plots for Section 1.1 #3
Tomorrow:
The main goal for this week has been to get some comfort with the context and computations we'll be working with throughout the course. This requires recalling some concepts and skills from calculus, linear algebra, and ordinary differential equations. In the process of working on problems, we've also seen glimpse of big ideas that we will see in more detail at various points in the course. Next week, we'll turn our attention to examples of how partial differential equations arise in the context of modeling real-world phenomena.
Topics: problem solution presentations (Katie M, Lizzi, Chris, Mitch, Amy, Jay)
Text: Section 1.1
Tomorrow: last problem solution presentations for Section 1.1; a few comments on Section 1.1 problems; density, flux, and conservation
The problems we saw today from Section 1.1 expose us to some big ideas that we'll explore in more detail at various points in the course. The main thing to gain from these problems right now is practice in working with functions, derivatives, and integrals in a multivariate context.
For reference, here is the handout on the Greek alphabet.
Topics: comments & questions on Gaussian and error function problems; a few more introductory remarks on PDEs
Text: Section 1.1
Mathematica: Plotting example: Gaussian functions
Tomorrow: problem solution presentations for Section 1.1
In class, we set up a schedule for the first round of problem solution presentations. We'll have the first presentations on Thursday and get through as many as time permits. If you have an assigned problem, be prepared to present on Thursday, although some presentations may get pushed to Friday if we run out of time. This handout has more details on expectations and requirements for problem solution presentations.
As part of looking at Gaussian functions and the error function, I used Mathematica to make some plots. In the next week, I'll be more deliberate in showing you how to use Mathematica as well as showing you some other options. Whenever we look at Mathematica work in class, I'll post a copy of the notebook we generate. To make use of these, you'll need access to a working copy of Mathematica. You can find Mathematica on most university computers. You can also access Mathematica (and other useful software) through vDesk, the university's new virtual desktop system..
Topics: course information; a comparison of ODEs and PDEs
Text: Section 1.1
Tomorrow: questions on Gaussian and error function problems; a few more introductory remarks on PDEs
In class, you started work on the first problem from the handout on Gaussian functions and the error function. As homework, you should work on all of the problems from this handout with two goals in mind: recalling some ideas and skills from calculus and getting an introduction to Gaussian functions and the error function. You can also have a quick read through Section 1.1 of the text.
On this course page, I will sometimes use typeset mathematical expressions using a system called MathJax. As an example, the quadratic formula is \[ x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}. \] Does the line above show a nicely formatted expression? If not, please send me a quick note telling me what platform (device, operating system, browser) you are using.
Here is a list of broad requirements and expectations for problem solution presentations.
| Name | Problem | Date |
|---|---|---|
| KM | Section 1.1 #2 | Thursday, September 1 |
| L | Section 1.1 #3 | Thursday, September 1 |
| CL | Section 1.1 #4 | Thursday, September 1 |
| M | Section 1.1 #5 | Thursday, September 1 |
| A | Section 1.1 #6 | Thursday, September 1 |
| J | Section 1.1 #7 | Thursday, September 1 |
| KR | Section 1.1 #9 | Friday, September 2 |
| C | ODE Review #3 | Thursday, September 8 |
| A | ODE Review #4 | Thursday, September 8 |
| CM | Density #1 | Friday, September 9 |
| Z | Flux #3 | Friday, September 9 |
| M | Section 1.2 #1 | Friday, September 9 |
| J | Section 1.2 #3 | Tuesday, September 13 |
| T | Section 1.2 #4 | Tuesday, September 13 |
| L | Section 1.2 #6 | Tuesday, September 13 |
| Z | Section 1.2 #7 | Tuesday, September 13 |
| S | Section 1.2 #5(a) | Thursday, September 15 |
| P | Section 1.2 #5(b) | Thursay, September 15 |
| Name | Problem | Date |
|---|---|---|
| J | Section 1.3 #3 | Thursday, September 22 |
| KM | Section 1.3 #4 | Friday September 23 |
| CL | Section 1.3 #5 | Friday September 23 |
| Z | Section 1.3 #6 | Friday September 23 |
| T | Section 1.3 #7 | Friday September 23 |
| M | Section 1.8 #1 | Friday September 30 |
| L | Section 1.8 #2 | Thursday September 29 |
| C | Section 1.8 #3 | Thursday September 29 |
| A | Section 1.8 #4 | Friday September 30 |
| S | Section 1.5 #3 | Friday September 30 |
| KR | Section 1.5 #4 | Friday September 30 |
| A | Section 1.5 #5 | Friday September 30 |
| J | Section 2.1 #1(a) | Tuesday October 11 |
| CM | Section 2.1 #1(b) | Tuesday October 11 |
| L | Section 2.1 #2 | Tuesday October 11 |
| Z | Section 2.1 #3 | Thursday October 13 |
| M | Section 2.1 #4 | Thursday October 13 |
| P | Section 2.1 #5 | Thursday October 13 |
| Name | Problem | Date |
|---|---|---|
| C | Section 3.2 #1 | Thursday, November 3 |
| KR | Section 3.2 #4 | Thursday, November 3 |
| L | Section 3.2 #5 | Thursday, November 3 |
| CL | Section 3.2 #8 | Thursday, November 3 |
| S | Section 3.3 #1 | Friday, November 4 |
| KM | Section 3.3 #2 | Friday, November 4 |
| A | Section 3.3 #3 | Friday, November 4 |
| A | Section 3.4 #3 | Tuesday, November 15 |
| T | Section 3.4 #4 | Tuesday, November 15 |
| L | Section 3.4 #6 | Tuesday, November 15 |
| P | Section 3.4 #7 | Tuesday, November 15 |
| J | Section 3.4 #8 | Thursday, November 17 |
| Z | Section 3.4 #9 | Thursday, November 17 |
| M | Section 3.4 #11 | Thursday, November 17 |
| J | Section 4.1 #3 | Friday, November 18 |
| M | Section 4.2 #1 | Friday, November 18 |
| C | Section 4.2 #2 | Monday, November 21 |
| Z | Section 4.2 #3 | Monday, November 21 |
"Can one hear the shape of a drum?"
Univeristy of New South Wales music acoustics web site
The Mathematical Atlas describes the many fields and subfields of mathematics. The site has numerous links to other interesting and useful sites about mathematics.
If you are interested in the history of mathematics, a good place to start is the History of Mathematics page at the University of St. Andrews, Scotland.
Check out the Astronomy Picture of the Day.