Daily notes
Tuesday, December 6
Topics: exam overview; questions on Fundamental Theorems problems
Text: Slides summarizing divergence and curl
Tomorrow: Exam #4
Today, we did some overview to begin preparing for the last exam. As part of that, we looked at these slides summarizing the big ideas of divergence and curl.
Exam #4 is on Friday, December 16 from 8 to 10 am. This handout has a list of specific objectives for the exam. For this exam, you can bring one sheet of notes (no bigger than a standard 8.5" by 11" sheet, both sides if you want). You must write your own notes. You are not allowed to photocopy, scan, or print directly from a source (including the course text and handouts). You can type up and then print your notes.
Below is a list of relevant handouts and corresponding subsections in the text. As I've noted previously, the approach we've taken in class differs somewhat from that of the text. In particular, the text approachs line and surface integrals strictly from a parametrization point of view. Our approach has been more geometric. In many cases, we end up parametrizing a curve (with one variable) or a surface (with two variables) without calling it this by name. In looking at the text, you might find the figures to be useful supplements to what I have been able to include in the handouts, particularly the last handout on the fundamental theorems.
- Integration over a surface
(Monday, November 14)
- Section 14.5 "Parametrizations of Surfaces"
- Section 14.5 "Surface Area"
- Skip Section 14.5 "Implicit Surfaces"
- Section 14.6 "Surface Integrals"
- Vector field plots
(Tuesday, November 15)
- Section 14.2 "Vector Fields"
- Section 14.2 "Gradient Fields"
- Integrating a vector field
over a curve
(Thursday, November 17)
- Section 14.2 "Work Done by a Force over a Curve in Space"
- Section 14.2 "Flow Integrals and Circulation for Velocity Fields"
- Skip Section 14.2 "Flux Across a Plane Curve"
-
Conservative vector fields
(Tuesday, November 22)
- Section 14.3 "Path Independence"
- Section 14.3 "Assumptions on Curves, Vector Fields, and Domains"
- Section 14.3 "Line Integrals in Conservative Fields"
- Section 14.3 "Finding Potentials for Conservative Fields"
- Skip Section 14.3 "Exact Differentials"
- Integrating a vector field
over a surface
(Tuesday, November 29)
- Section 14.6 "Orientation"
- Section 14.6 "Surface Integral for Flux"
- Skip Section 14.6 "Moments and Masses of Thin Shells"
- Divergence of a vector field
(Thursday, December 1)
- Section 14.4 "Divergence"
- Section 14.8 "Divergence in Three Dimensions"
- Curl of a vector field
(Friday, December 2)
- Section 14.4 "Spin Around an Axis: The k-component of Curl"
- Section 14.7 untitled first subsection on the curl vector
- Fundamental theorems of
calculus
(Monday, December 5)
- Section 14.4 "Two Forms for Green's Theorem" (but just the form in Theorem 5; skip the form in Theorem 4)
- Section 14.4 "Using Green's Theorem to Evaluate Line Integrals"
- Skip Section 14.4 "Proof of Green's Theorem for Special Regions"
- Section 14.7 "Stokes' Theorem"
- Section 14.7 "Paddle Wheel Interpretation of \(\vec\nabla\times\vec{F}\)" (just for the big picture, not the details)
- Skip Section 14.7 "Proof of Stokes' Theorem for Polyhedral Surfaces"
- Skip Section 14.7 "Stokes' Theorem for Surfaces with Holes"
- Section 14.7 "An Important Identity"
- Section 14.7 "Conservative Fields and Stokes' Theorem"
- Section 14.8 "Divergence Theorem"
- Skip Section 14.8 "Proof of the Divergence Theorem for Special Regions"
- Skip Section 14.8 "Divergence Theorem for Other Regions"
- Skip Section 14.8 "Gauss's Law: One of the Four Great Laws of Electromagnetic Theory" (unless you are a physics major)
- Skip Section 14.8 "Continuity Equation of Hydrodynamics" (unless you are a physics major)
- Section 14.8 "Unifying the Integral Theorems" (but note that we have not looked what the text calls the normal form of Green's Theorem)
All of the problems on Math 280 Exam 5 Spring 2011 are relevant to the material for our Exam #4. If you are looking for additional practice problems, here are some suggestions:
- Section 14.5 #17,19
- Section 14.2 #13,39
- Section 14.3 #5,29
- Section 14.6 #15,21
- Section 14.4 #17,19
- Section 14.7 #3,9
- Section 14.8 #5,9,17,21
Monday, December 5
Topics: questions on divergence and curl problems; the Fundamental Theorems of vector calculus
Text: Fundamental theorems of calculus and, optionally, the subsection on Stokes' Theorem in Sections 14.7, the subsection on the Divergence Theorem in Section 14.8, and the subsection on Green's Theorem in Section 14.4
Tomorrow: exam overview; questions on Fundamental Theorems problems
Over the past few weeks, we've seen various types of integral involving vector fields and we've seen two types of derivative for a vector field. Today, we looked at how how all of the pieces we've been developing over the past few weeks fit together into two important results: the Divergence Theorem and Stokes' Theorem. We also looked at the special case of Stokes' Theorem in the xy-plane that is called Green's Theorem. These results are fundamental theorems of calculus, all of which have the same basic structure: Integrating the derivative of a function over a region gives the same value as integrating the function itself over the edge of the region. In the case of a one-dimensional region such as a curve, the edge consists of only two points so integrating over the edge reduces to adding together two values.
This handout summarizes the fundamental theorems of calculus and has the assigned problems. The material on this is essential the same as what we saw on the slides in class.
For reference, here is the map of vector calculus that we have been looking at to see the big picture. On Monday, we'll finish off our journey by writing down the Fundamental Theorems of vector calculus.
Exam #4 is on Friday, December 16 from 8 to 10 am. I'll post a list of specific objectives here later today or early tomorrow.
Friday, December 2
Topics: questions on divergence problems; curl of a vector field
Text: Curl of a vector field and, optionally, the subsections on curl in Sections 14.4 and 14.7
Tomorrow: questions on divergence and curl problems; the Fundamental Theorems of vector calculus
Today, we looked at the curl of a vector field. For each point in the domain of the vector field, the curl is itself a vector. We defined the \(\hat{n}\) component of the curl as a circulation density for a planar loop with area vector in the \(\hat{n}\) direction. We defined this as a ratio of a circulation integral to area enclosed by the loop in a limit as the loop is shrunk to the point. This definition gives us insight on what curl tells us about a vector field. In particular, for the fluid flow interpretation, the \(\hat{n}\) component of curl at a point tells us the rotation rate of a paddlewheel anchored in fluid flow with axis oriented in the \(\hat{n}\) direction.
Computing curl directly from the definition as circulation density is feasible only for simple cases. In order to compute more generally, we developed a coordinate expression for the divergence of a vector field \(\vec{F}=P\,\hat{i}+Q\,\hat{j}+R\,\hat{k}\). That expressions turns out to be \[ \operatorname{curl}\vec{F} =\Bigl(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\Bigr) \,\hat{\imath} -\Bigl(\frac{\partial R}{\partial x}-\frac{\partial P}{\partial z}\Bigr) \,\hat{\jmath} +\Bigl(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\Bigr) \,\hat{k} \] Note: The choice here of writing the \(\hat\jmath\) component with a factor of \(-1\) pulled out is motivating by a way to think of the curl as the result of a cross product. Details on this and what we did in class today are on this handout. The handout also has some problems to give you practice with computing curl.
For reference, here is the map of vector calculus that we have been looking at to see the big picture. On Monday, we'll finish off our journey by writing down the Fundamental Theorems of vector calculus.
Thursday, December 1
Topics: questions on surface integral problems; divergence of a vector fields
Text: Divergence of a vector field and, optionally, the subsections on divergence in Sections 14.4 and 14.8
Tomorrow: questions on divergence problems; curl of a vector field
Today, we began looking at derivatives of vector fields. One starting point is to look at the partial derivatives of each component of a vector field \(\vec{F}\). Each partial derivative tells us how a particular component of \(\vec{F}\) changes with respect to change in a particular coordinate direction. Of the nine partial derivatives (for a vector field in space), two specific combinations turn out to be most important. We looked at the first of these today.
Our starting point for defining divergence of a vector field was to look at flux density at a point. We defined this as a ratio of a flux integral to volume enclosed by the surface in a limit as the surface is shrunk to the point. This definition gives us insight on what divergence tells us about a vector field. In particular, for the fluid flow interpretation, the value of divergence at a point tells us the (percentage) rate at which fluid volume is being created/injected into the flow. At a point where the divergence is positive, fluid is being created or injected into into the flow. At a point where the divergence is negative, fluid is being destroyed or sucked out of the flow.
Computing divergence directly from the definition as flux density is feasible only for simple cases. In order to compute more generally, we developed a coordinate expression for the divergence of a vector field \(\vec{F}=P\,\hat{i}+Q\,\hat{j}+R\,\hat{k}\). That expressions turns out to be \[ \operatorname{div}\vec{F}=\frac{\partial P}{\partial x} +\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}. \]
Details on what we did in class today are on this handout. The handout also has some problems to give you practice with computing divergence.
Tuesday, November 29
Topics: questions on Section 14.3 problems (the correct ones!); more on integrating a vector field over a surface
Text: Integrating a vector field over a surface and, optionally, Section 14.6
Tomorrow: questions on surface integral problems; derivatives of vector fields
In class, we continued discussing the idea of integrating a vector field over a surface. As with other types of integration, we can ask
- What is it?
- How do we compute it?
- What does it tell us?
Here's a quick take on each of these:
- What is it?
- Add up, over the surface, contributions of the form \(\vec{F}\cdot d\vec{A}\) or, equivalently, contributions of the form component of \(\vec{F}\) perpendicular to the surface times area of an infinitesimal piece of the surface.
- How do we compute it?
- Make a geometric argument (if the vector field and the surface have compatible symmetry); or
- Compute: Start by describing the surface in terms of two variables. Then work out the details of \(d\vec{A}=d\vec{r}_1\times d\vec{r}_2\) and \(\vec{F}\cdot d\vec{A}\) in terms of those two variables. Finally, set up and evaluate an iterated integral in the two variables.
- What does it tell us?
- If we interpret the vector field as a fluid flow velocity field \(\vec{v}\), then \(\displaystyle\iint_S\vec{v}\cdot d\vec{A}\) is the (time) rate at which fluid volume flows through the surface \(S\) in the direction of the vectors \(d\vec{A}\).
Project #2 is now due on Thursday, December 1. You should refer to the writing exercise handout and the notes on writing in mathematics for general directions.
Monday, November 28
Topics: questions on Section 14.3 problems; integrating a vector field over a surface
Text: Section 14.6
Tomorrow: more on integrating a vector field over a surface
We started class today with questions on Section 14.3 problems. Later in the day, I realized that I was reading off the problems from Section 14.2 rather than the ones from Section 14.3. So, we actually did Problems 25 and 27 from Section 14.2 using ideas from Section 14.3. Didn't anyone notice that something was off? Say something when I do something crazy like that in class! Tomorrow, we can look at Problems 25 and/or 27 from Section 14.3 if you want.
Our new idea for the day was integrating a vector field over a surface. We talked about what this means and we looked at one example in which we were able to evaluate the surface integral using a geometric argument. Tomorrow, we'll redo that example using a computational approach that is more general. I'll assign problems on this after class tomorrow.
Project #2 is now due on Thursday, December 1. You should refer to the writing exercise handout and the notes on writing in mathematics for general directions.
Tuesday, November 22
Topics: questions on Section 14.3 problems; potential functions, conservative vector fields, and the Fundamental Theorem for Line Integrals
Text: Section 14.3
Tomorrow: questions on Section 14.3 problems; integrating a vector field over a surface
Today, we discussed potential functions for vector fields and the Fundamental Theorem of Line Integrals. This FTC generalizes the familiar FTC that you learned earlier in your calculus career. Whereas any function of one variable that is continuous on an interval has an antiderivative defined on that interval, a vector field that is continuous on a region (of the plane or space) does not necessarily have a potential function. So, the FTC for line integrals is useful for integrating a vector field over a curve if there is a potential function for a region containing the curve and if we can find that potential function.
A vector field that has a potential function for a given region is said to be conservative for that region. The component test is often the easiest way to determine whether or not a vector field is conservative without directly looking for a potential function. The text states the component test using the notation \(\vec{F}=M\,\hat\imath+N\,\hat\jmath+P\,\hat{k}\). I prefer using \(\vec{F}=P\,\hat\imath+Q\,\hat\jmath+R\,\hat{k}\). In terms of this notation, the component test is stated as: A vector field \(\vec{F}=P\,\hat\imath+Q\,\hat\jmath+R\,\hat{k}\) is conservative (i.e., has a potential function) on a "nice" region if and only if \[ \frac{\partial R}{\partial y}=\frac{\partial Q}{\partial z}, \qquad \frac{\partial P}{\partial z}=\frac{\partial R}{\partial x}, \qquad\textrm{and}\qquad \frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y}. \]
In the context we are working, "nice" region means a region that is open, connected, and simply connected. You should read the relevant part of Section 14.3 for definitions of these.
Another way to characterize whether or not a vector field is conservative is to ask whether or not the value of a line integral for that vector field depends on the specific curve joining the endpoints. If the value of a line integral for a vector field is path-independent for all pairs of endpoints within a given region, then the vector field is conservative.
A final way to characterize whether or not a vector field is conservative is to look at the values of line integrals over closed loops. If the value of a line integral for a vector field is zero over every closed loop in the given region, then the vector field is conservative.
For reference, here is a handout summarizing these various ways to characterize a conservative vector field.
Those of you who are or will be taking physical chemistry might want to look at the subsection "Exact Differential Forms" since this language is sometimes used in that course. A differential \(P\,dx+Q\,dy+R\,dz\) is exact if it is the result of "d-ing" a function \(V\). In other words, a differential \(P\,dx+Q\,dy+R\,dz\) is exact if there is a function \(V\) so that \(dV=P\,dx+Q\,dy+R\,dz\). The question of whether or not a differential \(P\,dx+Q\,dy+R\,dz\) is exact is equivalent to the question of whether or not the vector field \(\vec{F}=P\,\hat\imath+Q\,\hat\jmath+R\,\hat{k}\) is conservative.
Project #2 is due on Tuesday, November 29. You should refer to the writing exercise handout and the notes on writing in mathematics for general directions.
Have a great break!
Monday, November 21
Topics: return Project #1; questions on Section 14.2 problems; is a given vector field the gradient of some function?
Text: Section 14.3
Tomorrow: questions on Section 14.3 problems; potential functions, conservative vector fields, and the Fundamental Theorem for Line Integrals
Today, we explored the question Given a vector field \(\vec{F}\), is there a function \(f\) such that \(\vec{F}\) is the gradient of \(f\)?. In other words, is there a function \(f\) such that \(\vec{F}=\vec\nabla f\)? We saw at least one example in which there is such a function for the given vector field. In this case, we say that the function \(f\) is a potential function for the vector field \(\vec{F}\). We also say that the vector field itself is conservative. We also saw at least one example in which there is no such function for the give vector field \(\vec{F}\). In this case, we say that the vector field is not conservative.
The language of potential function and conservative vector field comes from physics. If we wanted to use language that parallels antiderivative, we might say that \(f\) is an antigradient of the vector field \(\vec{F}\) if \(\vec\nabla f=\vec{F}\). However, the word antigradient is not in standard use.
Tomorrow, we will be a bit more careful with conditions on domains for \(\vec{F}\) and \(f\). We'll also state and use the Fundamental Theorem of Calculus for Line Integrals which gives us a way to evaluate line integrals using a potential function (if the vector field is conservative).
I've assigned just two problems from Section 14.3. I'll assign additional problems after class tomorrow.
Project #2 is due on Tuesday, November 29. You should refer to the writing exercise handout and the notes on writing in mathematics for general directions.
Friday, November 18
Topics: more on integrating a vector field along a curve
Text: Integrating a vector field along a curve and Section 14.2
Tomorrow: questions on Section 14.2 problems; potential functions, conservative vector fields, and the Fundamental Theorem for Line Integrals
In class, we continued discussing the idea of integrating a vector field over a curve. As with other types of integration, we can ask
- What is it?
- How do we compute it?
- What does it tell us? (or How is it used?)
Today, we addressed the latter two questions and got some practice in computing. You will need to get more practice by doing the assigned problems from the handout "Integrating a vector field along a curve" and Section 14.2. As you work on these problems, try to visualize each vector field and curve so you can use your geometric intuition to get some sense of what value to expect for the integral.
Project #2 is due on Tuesday, November 29. You should refer to the writing exercise handout and the notes on writing in mathematics for general directions.
Thursday, November 17
Topics: return Exam #3; questions on Section 14.2 problems; integrating a vector field along a curve
Text: Integrating a vector field along a curve and Section 14.2
Tomorrow: more on integrating a vector field along a curve
In class, we started discussing the idea of integrating a vector field over a curve. As with other types of integration, we can ask
- What is it?
- How do we compute it?
- What does it tell us? (or How is it used?)
Today, we only had time to address "What is it?" and give a very brief idea of "What does it tell us?. Tomorrow, we'll get practice in computing and use specific results to get a better feel for what this type of integration tells us. If you want a preview, you can look at this handout on integrating a vector field along a curve. You can wait until after class tomorrow to work on the problems from this handout and the new assignment for problems from Section 14.2.
Project #2 is due on Tuesday, November 22. You should refer to the writing exercise handout and the notes on writing in mathematics for general directions.
Tuesday, November 15
Topics: questions on surface integration problems; vector fields
Text: Section 14.2
Tomorrow: questions on Section 14.2 problems; integrating a vector field along a curve
Today, we began looking at vector fields. For much of the course, we have been working with scalar fields (without using this name). A scalar field assigns a number (i.e., a scalar) to each point in a given domain (which can be part of a line, a plane, or space). A vector field assigns a vector to each point in a given domain (which can be part of a line, a plane, or space). Examples of scalar fields include temperature, presssure, and density. Examples of vector fields include velocity, force, and electric fields. In class, we looked at this surface air velocity vector field.
For the last part of the course, we will study the calculus of vector fields. Today, we got a bit of practice visualizing some basic planar vector fields on this handout. As homework, you should finish these problems and work on the assigned problems from Section 14.2. On Thursday, we will look at the idea of integrating a vector field along a curve.
Project #2 is due on Tuesday, November 22. You should refer to the writing exercise handout and the notes on writing in mathematics for general directions.
Monday, November 14
Topics: questions on Section 10.4 problems; more on integrating over a surface
Text: Integrating over a surface and, optionally, Section 14.5
Tomorrow: questions on surface integration problems; vector fields
In class, we looked at integrating over a surface. A key part of evaluating a surface integral is expressing the area element dA in terms of the coordinates chosen to describe the surface. In the simplest cases, we can use a geometric argument to deduce an expression for dA. In other cases, we need a computational approach. The basic idea and some examples are on this handout. The handout also has the assigned problems for this material.
As with integrating over a curve, we will follow an approach that differs somewhat from the main approach used in the text. The text approaches integrating over curves and surfaces in terms of parametrizing the curve or surface. Our approach is a bit more general. You are welcome to read about the text's approach to integrating over a curve in Section 14.1 and integrating over a surface in Section 14.5.
Project #2 is due on Tuesday, November 22. You should refer to the writing exercise handout and the notes on writing in mathematics for general directions.
Friday, November 11
Topics: first example of integrating over a surface; cross product
Text: Section 10.4
Tomorrow: questions on Section 10.4 problems; more on integrating over a surface
We started class with a first example of integrating over a surface. As part of this, we needed to describe the surface in terms of a chosen coordinate system and then work out an expression for the area element of the surface in that coordinate system. For the first example, the surface was a sphere and we were able to use a geometric argument to deduce an expression for the area element in spherical coordinates. We will develop a more general approach for more general situations. As part of that, we will use a new tool called the cross product of two vectors.
In the latter part of class, we defined the cross product of two vectors. The cross product of \(\vec{u}\) and \(\vec{v}\) is a new vector denoted \(\vec{u}\times\vec{v}\) and defined geometrically in relationship to the parallelogram that has \(\vec{u}\) and \(\vec{v}\) as its edges. Specfically, \(\vec{u}\times\vec{v}\) is defined geometrically by these two properties:
- The direction of \(\vec{u}\times\vec{v}\) is perpendicular to the \(\vec{u}\vec{v}\)-parallelogram so that \(\{\vec{u},\vec{v},\vec{u}\times\vec{v}\}\) has a right-hand orientation.
- The magnitude of \(\vec{u}\times\vec{v}\) is the area of the \(\vec{u}\vec{v}\)-parallelogram.
From this definition, it is straightforward to work out the cross product for each pair of the unit coordinate vectors \(\hat\imath\), \(\hat\jmath\), \(\hat k\). For example, \(\hat k\times\hat\imath=\hat\jmath\). Algebraic properties of the cross product include
| anticommutative property: | \(\vec{u}\times\vec{v}=-\vec{v}\times\vec{u}\) |
| distributive property: | \(\vec{u}\times(\vec{v}+\vec{w}) =\vec{u}\times\vec{v}+\vec{u}\times\vec{w}\) |
| scalar factor property: | \(\alpha(\vec{u}\times\vec{v})=(\alpha\vec{u})\times\vec{v} =\vec{u}\times(\alpha\vec{v})\) |
Using these properties and results for crossing pairs of unit coordinate vectors, we can compute the cross product of any two vectors in terms of their cartesian components.
In Section 10.4 of the text, the authors show another way of computing cross products that uses determinants. You can ignore that method if you wish (particularly if you have not seen previously seen determinants.) The determinant method is essentially equivalent to the "shortcut" method we used in the example at the end of class.
Project #2 is due on Tuesday, November 22. You should refer to the writing exercise handout and the notes on writing in mathematics for general directions.
Thursday, November 10
Topics: Exam #3
Text: Sections 13.1-13.5, 13.6, Integration over a curve
Tomorrow: integrating over a surface; a second way to multiply vectors
Tuesday, November 8
Topics: questions on curve integration problems
Text: Integration over a curve
Tomorrow: Exam #3
Today, we addressed questions from the curve integration problems.
Exam #3 will be on Thursday November 10. We will use the 80-minute period from 8:00 to 9:20. The exam will cover material from Sections 13.1-13.6, 13.7, and the curve integration handout. This handout has a list of specific objectives for the exam. All of the problems on the Spring 2011 Exam #4 are relevant to this material. Note that the exam will not include the Lagrange multiplier approach to constrained optimization (Section 12.8).
I have reserved TH 381 (next to our usual classroom) starting at 7 pm on Wednesday November 9 for an informal Math 280 study session. If you are looking for others to study with, come to the classroom after 7 pm and find a small group working on something of interest.
Monday, November 7
Topics: questions on volume density problems
Text: Integration over a curve
Tomorrow: exam overview; questions on curve integration problems
Today, we addressed questions from the volume density problems. Tomorrow, we'll look at questions from the curve integration problems.
Exam #3 will be on Thursday November 10. We will use the 80-minute period from 8:00 to 9:20. The exam will cover material from Sections 13.1-13.6, 13.7, and the curve integration handout. This handout has a list of specific objectives for the exam. All of the problems on the Spring 2011 Exam #4 are relevant to this material. Note that the exam will not include the Lagrange multiplier approach to constrained optimization (Section 12.8).
Friday, November 4
Topics: questions on second set of Section 13.7 problems; integrating over a curve
Text: Integration over a curve
Tomorrow: questions on volume density problems; questions on curve integration problems (as time allows)
Today, we looked at the idea of integrating over a curve. Here, we will be thinking about a curve in the plane or in space that we (conceptually) break into small pieces each of which has a length ds. In some cases, we will add up these small contributions to get the total length of the curve. In other cases, we will have a length density λ defined at each point on the curve and we will add up small contributions of the form λds to get a total (of some quantity such as charge or mass). This handout has some details and the assigned problems.
Exam #3 will be on Thursday November 10. We will use the 80-minute period from 8:00 to 9:20. The exam will cover material from Sections 13.1-13.6, 13.7, and the curve integration handout. This handout has a list of specific objectives for the exam. All of the problems on the Spring 2011 Exam #4 are relevant to this material.
Thursday, November 3
Topics: questions on Section 13.7 problems; spherical coordinates; iterated integrals in spherical coordinates
Text: Section 13.7
Tomorrow: questions on second set of Section 13.7 problems; integrating over a curve
In class, we discussed spherical coordinates. As part of this, you worked through this handout to make a geometric argument for the volume element in spherical coordinates. We then put this result to use by setting up an iterated integral in spherical coordinates to compute the volume of a sphere of radius R.
I've assigned additional problems from Section 13.7 that deal with iterated integrals in spherical coordinates.
Exam #3 will be on Thursday November 10. We will use the 80-minute period from 8:00 to 9:20.
Tuesday, November 1
Topics: questions on Section 13.5 problems; iterated integrals in cylindrical coordinates
Text: Section 13.7
Tomorrow: questions on Section 13.7 problems; iterated integrals in spherical coordinates
In class, we looked at an example of setting up and evaluating an iterated integral in cylindrical coordinates. You can think of cylindrical coordinates as polar coordinates r and θ for a plane together with a third coordinate z measuring the distance away from that plane. I've assigned some problems from Section 13.7. I'll assign additional problems from this section after we discuss spherical coordinates.
We will not cover the material in Section 13.6 in any detail. One of the ideas in that section is getting total mass given mass density. We have already woven that theme into our study of integration. The other ideas in Section 13.6 are center of mass and moments of inertia (aka rotational inertia). Those of you who have or are taking a first-year physics course might want to have a look at these sections to see connections between our course and your physics course.
Exam #3 will be on Thursday November 10. We will use the 80-minute period from 8:00 to 9:20.
Monday, October 31
Topics: questions on Section 13.4 problems; triple integrals and iterated integrals in cartesian coordinates
Text: Section 13.5
Tomorrow: questions on Section 13.5 problems; iterated integrals in cylindrical coordinates
Today, we looked at examples of triple integrals and the corresponding iterated integrals in three variables. A triple integral involves adding up infinitely many infinitesimal contributions to a total over a region of space. To describe this type of region, we need a three-dimensional coordinate system so we end up with an iterated integral in three variables (that is, the three coordinate variables). For the example we looked at today, we used cartestian coordinates. In some other example, we might find it convenient to use some other coordinate system. This week, we will look at two other coordinate systems for three dimensions: cylindrical coordinates and spherical coordinates.
Exam #3 will be on Thursday November 10. We will use the 80-minute period from 8:00 to 9:20.
Friday, October 28
Topics: questions on Section 9.1 and 9.2 problems; iterated integrals in polar coordinates
Text: Section 13.4
Tomorrow: questions on Section 13.4 problems; triple integrals
Today, we looked another example of evaluating a double integral using an iterated integral in polar coordinates. To set up an interated integral in polar coordinates (r,θ), we need to do three things:
- Describe the region with appropriate bounds on r and θ (with at least one of the two having constant bounds).
- Find an expression for the integrand in terms of r and θ.
- Use dA=rdrdθ or dA=rdθdr with the choice dictated by which of the variables has constant bounds.
Project #1 is due on Monday, October 31. You should refer to the writing exercise handout and the notes on writing in mathematics for general directions.
Thursday, October 27
Topics: questions on area density problems; polar coordinates; plotting polar curves
Text: Sections 9.1 and 9.2
Tomorrow: questions on Section 9.1 and 9.2 problems; iterated integrals in polar coordinates
Today, we discussed the basics of polar coordinates and plotting polar curves. The animation below shows the curve r=cos(2θ) being traced out as θ increases. Tomorrow, we'll address questions from Section 9.1 and 9.2 problems. If this does not provide you with enough comfort using polar coordinates, we can arrange a time to talk outside of class.
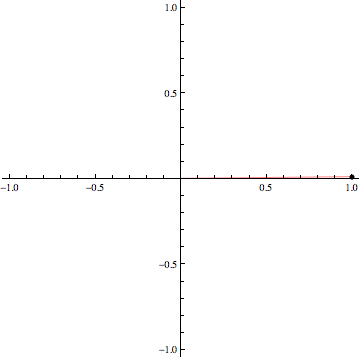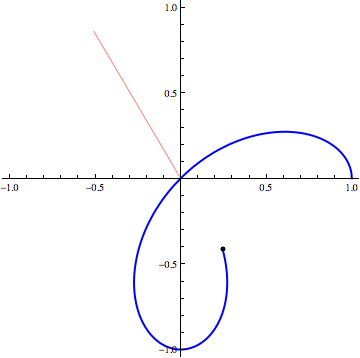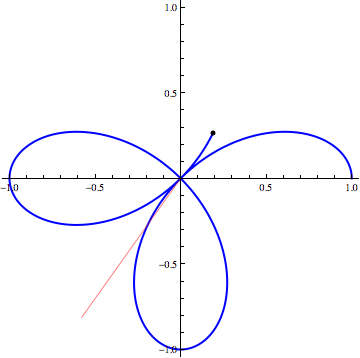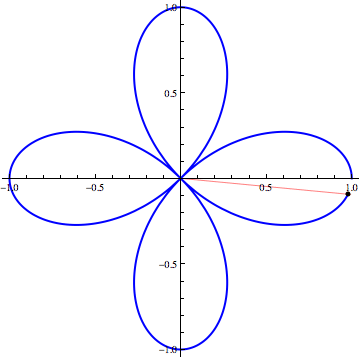
Many graphing calculators have a polar graphing feature. On a TI-8X, you can get to this by going to the MODE menu and choosing the option Pol from the list Func Par Pol Seq. If you then go to the Y= menu, you will see r1= where you can enter a formula for a polar curve. In Mathematica, you can plot a polar curve using the PolarPlot command. On WolframAlpha, you can just type in the polar relation.
Project #1 is due on Monday, October 31. You should refer to the writing exercise handout and the notes on writing in mathematics for general directions.
Tuesday, October 25
Topics: questions on Section 13.2 problems; iterated integrals in polar coordinates
Text: Section 13.4
Tomorrow: questions on area density problems; more on polar coordinates and iterated integrals in polar coordinates
Today, we looked at evaluating a double integral using an iterated integral in polar coordinates. To set up an interated integral in polar coordinates (r,θ), we need to do three things:
- Describe the region with appropriate bounds on r and θ (with at least one of the two having constant bounds).
- Find an expression for the integrand in terms of r and θ.
- Use dA=rdrdθ or dA=rdθdr with the choice dictated by which of the variables has constant bounds.
Different people will bring different levels of familiarity with polar coordinates to this course. On Thursday, we'll talk a bit more about the basics of polar coordinates and then look at another example or two of setting up and evaluating iterated integrals in polar coordinates.
Your new homework assignment consists of problems that involve computing a total from an area density. You can wait until later to look at Problem 5 from this assignment since it is best done using polar coordinates.
Project #1 is due on Friday, October 28. You should refer to the writing exercise handout and the notes on writing in mathematics for general directions.
Monday, October 24
Topics: questions on Section 13.1 problems; double integrals over non-rectangular regions
Text: Section 13.2
Tomorrow: questions on Section 13.2 problems; iterated integrals in polar coordinates
Today, we looked at double integrals over non-rectangular regions. To set up an equivalent iterated integral, we need to describe the region with bounds on the cartesian coordinates x and y. If the region is rectangular, we will have constant lower and upper bounds on both x and y. If the region is not rectangular, we will have constant lower and upper bounds on either x or y and at least one nonconstant bound on the other one. The variable with constant bounds must be the outer variable in the iterated integral. In some cases, it is best to split the original region into smaller pieces and to then describe each piece with appropriate bounds on x and y.
Project #1 is due on Friday, October 28. You should refer to the writing exercise handout and the notes on writing in mathematics for general directions.
Friday, October 21
Topics: questions on nonuniform density problems; double integrals; evaluating a double integral using an iterated integral
Text: Section 13.1
Tomorrow: questions on Section 13.1 problems; double integrals over non-rectangular regions
Today, we began looking at multivariable integration. In particular, we looked at double integrals. A double integral involves adding up infinitely many infinitesimal contributions over a two-dimensional region. A double integral of the function f over the region R is denoted \[ \iint\limits_{R}f\,dA. \] To evaluate a double integral, we will choose a coordinate system and set up an equivalent iterated integral. In cartesian coordinates, we will have either \[ \int_a^b\int_c^d f(x,y)\,dydx \qquad\textrm{or}\qquad \int_c^d\int_a^b f(x,y)\,dxdy. \] Fubini's Theorem states that if f is continuous throughout R, then \[ \iint\limits_{R}f\,dA=\int_a^b\int_c^d f(x,y)\,dydx = \int_c^d\int_a^b f(x,y)\,dxdy. \] So, we can evaluate a double integral of a continuous function by setting up and evaluating either of the corresponding iterated integrals. Each of the iterated integrals represents a particular way or organizing the "adding up" represented by the double integral. Typically, we will evaluate an iterated integral by successively applying the Fundamental Theorem of Calculus.
In Section 13.1, the authors approach double and iterated integrals within the context of computing volume for a solid region bounded by the graph of a function of two variables. This generalizes the idea of computing area for a planar region bounded by the graph of a function of one variable. In class, we will put more focus on the "total from density" interpretation/application because this context is relevant in other settings. The "area under a curve" or "volume under a surface" interpretation/application is less readily generalized to higher dimensions.
For reference, here is the handout on the Greek alphabet that we looked at briefly in class.
Project #1 is due on Friday, October 28. You should refer to the writing exercise handout and the notes on writing in mathematics for general directions.
Thursday, October 20
Topics: questions on Section 12.8 problems; integration
Text: Nonuniform density
Tomorrow: questions on nonuniform density problems; integration in more than one variable
After looking at a homework problem, I gave a quick overview of Mathematica. You can Mathematica on many computers on campus or you can access it through vDesk from your own computer. vDesk is a virtual desktop system that the university launched over the summer. After you log on to vDesk, go to the Academic Applications folder and then to the Computer Science and Math Applications folder. Launching an application through vDesk takes a bit of time but the application generally runs at a reasonable pace once it has launched.
The best way to get started with something like Mathematica is to experiment. This handout has a list of inputs you can try in Mathematicato get a sense of what is possible. To help you get started, I will be in the TH 189 computer lab from 3:00 to 4:00 today (Thursday) and for office hour from 9:00 to 10:00 tomorrow (Friday). If you are interested and have time, come experiment with Mathematica while I am there to answer questions.
You can also get to some of Mathematica's capabilities online through the WolframAlpha web site. (Wolfram is the company that produces Mathematica. WolframAlpha is a web-based service to provide information and do computations.) At the WolframAlpha site, you can enter Mathematica commands or just try natural language. Mathematica commands will be interpreted without ambiguity whereas natural language input generally has some ambiguity that might be interpreted in a way other than what you have in mind.
In class, we also began our discussion of integration. At a fundamental level, integration is adding up infinitely many infinitesimal contributions to a total. In your first look at integration, you probably focused on one main application, namely computing area under a curve. You can think about this as computing the area for a "rectangle with variable height". You might also have use integration to compute a total accumulation from a variable accumulation rate. In this course, we will use a third context as our primary application: using integration to compute a total amount of stuff from a density for that stuff.
Your first introduction to density (a long time ago) likely came as something like "density is mass divided by volume". Turning this around, we can say "mass is density times volume". Getting a total mass from a density by multiplication works for situations with uniform density. For nonuniform density, we will get a total from a density using integration.
In addition to generalizing to nonuniform density, 0ur use of density will be more general than your initial view in two other ways:
- other dimension: length, area, or volume
- other quantities: mass, number, charge, cost, probability,...
To denote a length density, we will typically use \(\lambda\) (the Greek letter "lambda"). For area density, we will generally use \(\sigma\) (the Greek letter "sigma"). For the more familiar volume density, we will use either \(\rho\) (the Greek letter "rho") or \(\delta\) (the Greek letter "delta").
If the stuff (mass, number, charge,...) is spread out uniformly, then we can get the total amount of stuff by multiplication. If the stuff is not spread out uniformly, we need integration to compute the total amount of stuff. In class, we looked at doing this with stuff spread out on a line segment. This handout has related examples and problems.
Project #1 is due on Friday, October 28. You should refer to the writing exercise handout and the notes on writing in mathematics for general directions.
Friday, October 14
Topics: constrained optimization using the method of Lagrange multipliers
Text: Section 12.8 and slides on constrained optimization
Tomorrow: questions on Section 12.8 problems; integration
Today we looked at approaching constrained optimization problems using the method of Lagrange multipliers. This method is motivated geometrically by looking for points at which a level curve/surface of the objective function is tangent to the constraint curve/surface. This is equivalent to points at which the objective function gradient vector is aligned with the constraint function gradient vector.
Project #1 is due on Friday, October 28. You should refer to the writing exercise handout and the notes on writing in mathematics for general directions.
Have a great Fall Break!
Thursday, October 13
Topics: Exam #2
Text: Sections 10.2, 10.3, the second planes handout, 11.1, 11.3, 12.5, 12.6, and 12.7.
Tomorrow: constrained optimization using the method of Lagrange multipliers
Tuesday, October 11
Topics: exam overview; questions on applied optimization problems
Text: Sections 10.2, 10.3, the second planes handout, 11.1, 11.3, 12.5, 12.6, and 12.7
Tomorrow: Exam #2
Exam #2 will be on Thursday October 13. We will use the 80-minute period from 8:00 to 9:20. The exam will cover material from Sections 10.2, 10.3, the second planes handout, 11.1, 11.3, 12.5, 12.6, and 12.7. This handout has a list of specific objectives for the exam. You might also want to look at questions from old exams. Since we have covered the material in a different order than previous course offerings, I have put together this composite of Exams #1 and #2 from Spring 2011. Most problems on the Spring 2011 Exam #3 are also relevant with the exception of Problem 6.
I will be available for office hour today (Tuesday) from 12:30 to 1:30 and for appointments after that until at least 4:30. On Wednesday, I will time in the morning and after 2:00. If you have questions, email or call to set up a time to talk. I can address questions sent by email.
I have reserved TH 381 (next to our usual classroom) starting at 7 pm on Wednesday October 13 for an informal Math 280 study session. If you are looking for others to study with, come to the classroom after 7 pm and find a small group working on something of interest.
Monday, October 10
Topics: questions on Section 12.7; applied optimization
Text: Section 12.7
Tomorrow: exam overview; questions on applied optimization problems
Today, you worked in groups on the first problem or two from this handout. The remaining problems are your homework assignment for today. In applied optimization problems, you must often first build the relevant function. Part of this involves identifying the relevant independent variables. In some contexts, there is a constraint that relates variables. If so, you can use the constraint to eliminate one of the variables and thus reduce the number of independent variables. Once you have built the function in terms of the truly independent variables, you can look for the relevant extreme value. As part of setting up the function to be optimized, you should also set up any domain restrictions on the independent variables.
Exam #2 will be on Thursday October 13. We will use the 80-minute period from 8:00 to 9:20. The exam will cover material from Sections 10.2, 10.3, the second planes handout, 11.1, 11.3, 12.5, 12.6, and 12.7. This handout has a list of specific objectives for the exam. You might also want to look at questions from old exams. Since we have covered the material in a different order than previous course offerings, I have put together this composite of Exams #1 and #2 from Spring 2011. [Note: I updated this composite on Tuesday morning to include some problems I initially overlooked and some problems on vector-valued functions from older exams.] Most problems on the Spring 2011 Exam #3 are also relevant with the exception of Problem 6.
Friday, October 7
Topics: using the second-derivative to classify critical points; global extreme values
Text: Section 12.7
Tomorrow: questions on Section 12.7; applied optimization
Today, we first discussed the second-derivative test. To better understand why the second-derivative test works, we put together two pieces:
- the Taylor series expansion of \(f\) based at the critical point \((x_0,y_0)\) and
- functions of the form \(Au^2+2Buv+Cv^2\) for various choices of the constants \(A\), \(B\), and \(C\).
We then turned our attention to global extreme values. As with local extreme values, we want to distinguish between what it is and how to find it. "What it is" for global extreme values is given by the following definition.0
Definition: Given a function \( f:\mathbb{R}\to\mathbb{R}\) we say an input \((x_0,y_0)\) is a global maximizer and the corresponding output \(f(x_0,y_0)\) is a global maximum for a given region \(R\) if \(f(x_0,y_0)\geq f(x,y)\) for all \((x,y)\) in \(R\). Global minimizer and global minimum are defined similarly with the inequality reversed.
"How to find it" for global extreme values generally consists of putting together a list of outputs to compare. To generate this list, we need to find all critical points that are in the interior of the region \(R\) and we need to analyze \(f\) along the boundary of \(R\). In class, we started an example of this but did not finish. This handout has the full details on that example.
Exam #2 will be on Thursday October 13. We will use the 80-minute period from 8:00 to 9:20.
Thursday, October 6
Topics: questions on differentials problems; extreme values
Text: Section 12.7
Tomorrow: using the second-derivative to classify critical points; global extreme values
In class, we looked at local extreme values. In thinking about extreme values, we want to distinguish between what it is and how to find it.
"What it is" for local extreme values is given by the following definition.
Definition: Given a function \( f:\mathbb{R}\to\mathbb{R}\) we say an input \((x_0,y_0)\) is a local maximizer and the corresponding output \(f(x_0,y_0)\) is a local maximum if there is an open disk centered at \((x_0,y_0)\) such that \(f(x_0,y_0)\geq f(x,y)\) for all \((x,y)\) in that disk. Local minimizer and local minimum are defined similarly with the inequality reversed.
"How to find it" for local extreme values generally consists of two steps:
- Find all critical points by solving the system of equations given by setting the two first-partial derivatives equal to zero.
- Analyze each critical point to classify it as a local minimizer, a local maximizer, or neither. For this, use either direct analysis or the second-derivative test.
We have not yet looked at how the second-derivative test works for functions of two variables. We'll do so tomorrow. We'll also look at global extreme values.
I've assigned a few problems from Section 12.7. For now, focus on finding the critical points for each of the given functions. After class tomorrow, you can finish these problems by using the second-derivative test to classify each critical point as a local minimum, a local maximum, or a saddle. I'll also assign a few more problems that deal with finding global extreme values.
Exam #2 will be on Thursday October 13. We will use the 80-minute period from 8:00 to 9:20.
Tuesday, October 4
Topics: questions on Section 12.6 problems; differentials
Text: Section 12.6
Tomorrow: questions on differentials problems; extreme values
In class, we looked at how to use differentials to relate (infinitesimally) small changes among variables. Generally, we start with a nonlinear relation among various variables and we then compute a linear relation among the differentials for those variables. Differentials can be thought of as coordinates in the "zoomed-in world". Differentials are always related linearly. Ratios of differentials give rates of change. No limit is needed since the limit process has already been taken care of in "zooming in" process.
Working with differentials complements working with the linearization function L. Differentials are useful when we want to focus on change and rate of change. Linearizations are useful when we want to focus on approximating specific output values.
Monday, October 3
Topics: more questions on Section 12.5 problems; tangent planes and linearization
Text: Section 12.6
Tomorrow: differentials
In class, we reviewed tangent lines for functions of one variable and then considered tangent planes for functions of two variables. We then recast these ideas in terms of linearization. The linearization of a function f is a linear function L built using information about f at a specific point (x0,y0). If the function is differentiable at a point, then the linearization based at that point is the best linear approximation. There are many contexts in which one trades in the full accuracy of a function for the simplicity of the linearization. In making this trade, it is often essential to have some handle on how much error is introduced by trading in for the linearization. We looked at an error bound for the linearization of a function of one variable. There is a similar error bound for the linearization of a function of two variables. In class, we did not do an example of getting an upper bound on the error in a linearization for a function of two variables. I've written up the details of an example in this handout. You might find this useful in looking at Problem 33 from Section 12.6.
The text's approach to tangent planes and linearization for functions of two variables differs from what we did in class. The text starts with the more general idea of a tangent plane to a surface at a point where that surface is not necessarily the graph of a function z=f(x,y). In reading Section 12.6, you can focus on
- Example 2 on page 749 and the box just above that example
- The subsection "How to linearize a function of two variables" on pages 751-752
- The subsection "Functions of more than two variables"
For reference, here's the applet we looked at in class that allows you to look at tangent planes for the graph of a function of two variables.
Tomorrow, we will talk about differentials. This will provide us with a clean and powerful way to look at the linear relations that underlie linearization.
Friday, September 30
Topics: questions on Section 12.5 problems; gradient vector fields; differentiability
Text: Section 12.5
Tomorrow: more questions on Section 12.5 problems; tangent planes and linearization
Many of the problems on gradient from the text involve looking at a single gradient vector. To emphasize that there is a gradient vector at each point in the domain, we drew a gradient vector field for the first problem on this handout. As homework, you should complete the two problems on the handout.
At the end of class, we had a quick look at what differentiability means by first reviewing the idea for functions of one variable and then thinking about how this generalizes to functions of two variables. Geometrically, we will think of a function of two variable as being differentiable at a point if zooming in on the graph of the function for that point results in a plane. This is a tangent plane. We'll talk about equations of tangent planes on Monday.
Many of you did not have/take time to look deeply at the Section 12.5 problems before class today. So, we'll take a few minutes at the beginning of class on Monday to address more questions and I've pushed back the due date for the problems to be submitted until Tuesday.
Thursday, September 29
Topics: gradient vectors and directional derivatives
Text: Section 12.5
Tomorrow: questions on Section 12.5 problems; tangent planes and linearization
In class, we continued discussing greatest rate of change. In particular, we
- reviewed the definition of gradient vector that we set up on Tuesday, and
- determined how to compute the components of a gradient vector (in cartesian coordinates).
While the reasoning we went through to connect these two things may initially be challenging, the take-away messages are simple:
- The gradient at each point is a vector \(\vec\nabla f\)
- that points in the direction of greatest rate of change, and
- has magnitude equal to that greatest rate of change.
- In cartesian coordinates, components of gradient vectors are computed as \(\displaystyle \vec\nabla f=\frac{\partial f}{\partial x}\hat{\imath}+ \frac{\partial f}{\partial y}\hat{\jmath}. \)
Here's a handout outlined the reasoning we discussed in class. A key part of this reasoning is that infinitesimal changes \(df\) in outputs are related to infinitesimal displacements \(d\vec{r}\) by \( df=\vec\nabla f\cdot d\vec{r}\).
This last relation also forms a starting point for thinking about directional derivative. For a function f, we can ask about the rate of change at a particular point in a particular direction. We denote the directional derivative as \(df/ds\) where df represents an infinitesimal rise and ds represents an infinitesimal run. We can compute a directional derivative by finding the component of the gradient vector along the direction of interest. If the unit vector \(\hat{u}\) gives the direction of interest, then the directional derivative is given by \[ \frac{df}{ds}=\vec{\nabla} f\cdot\hat{u}. \] An alternate notation for direction derivative is \(D_{\hat{u}}f\). With this, we can write the result as \[ D_{\hat{u}}f=\vec{\nabla} f\cdot\hat{u}. \] Note that we can think of a directional derivative as the component of the gradient vector in the direction \(\hat{u}\).
The writing exercise is due Friday, September 30.
Tuesday, September 27
Topics: questions on 11.3 problems; greatest rate of change
Text: Section 12.5
Tomorrow: computing greatest rate of change
In class, we discussed the idea of greatest rate of change for a function \(f\) of two or more variables. We started with this handout on estimating greatest rate of change for a function of two variables. Since greatest rate of change involves both direction and magnitude, we represent the greatest rate of change as a vector at each point in the domain of the function. These are called gradient vectors and denoted \(\vec\nabla f\). So, at each point in the domain of the function, a gradient vector
- points in the direction of greatest rate of change
- has magnitude equal to that greatest rate of change.
On Thursday, we'll talk about how to compute the gradient of a function if we are given a formula for the function.
In class, I occasionally use Mathematica to make pictures and do calculations. If you are interested in Mathematica, you can find it on many computers on campus or you can access it through vDesk from your own computer. vDesk is a virtual desktop system that the university launched over the summer. After you log on to vDesk, go to the Academic Applications folder and then to the Computer Science and Math Applications folder. Launching an application through vDesk takes a bit of time but the application generally runs at a reasonable pace once it has launched.
You can also get to some of Mathematica's capabilities online through the WolframAlpha web site. (Wolfram is the company that produces Mathematica. WolframAlpha is a web-based service to provide information and do computations.) At the WolframAlpha site, you can enter Mathematica commands or just try natural language. Mathematica commands will be interpreted without ambiguity whereas natural language input generally has some ambiguity that might be interpreted in a way other than what you have in mind.
The writing exercise is due Friday, September 30.
Monday, September 26
Topics: questions on 11.1 problems; infinitesimal displacement vectors; length of a curve
Text: Section 11.3
Tomorrow: questions on 11.3 problems; greatest rate of change
In class, we looked at the idea of infinitesimal displacement vectors. We denote an infinitesimal vector as \(d\vec{r}\) and we express it in terms of components as \[ d\vec{r}=dx\,\hat\imath+dy\,\hat\jmath \qquad\textrm{or}\qquad d\vec{r}=dx\,\hat\imath+dy\,\hat\jmath+dz\,\hat k \] depending on whether we are working in two or three dimension. Along a curve, the components \(dx\), \(dy\), and \(dz\) are related to each other. If the curve is described parametrically in terms of a parameter \(t\), then the components \(dx\), \(dy\), and \(dz\) are related to \(dt\). In this case, we can express the general relationship as \[ d\vec{r}=\vec{r}^\prime(t)\,dt. \] Thinking in terms of time \(t\), position \(\vec{r}(t)\), and velocity \(\vec{r}^\prime(t)\), this says that an infinitesimal displacement along a curve is a velocity times an infinitesimal increment in time.
If we add up infinitesimal displacements along a curve, we get the total displacement. This is nothing more than the displacement from the start position to the end position. A more interesting problem is to calculate the length of a curve by adding up magnitudes of infinitesimal displacements along the curve. A common notation for the magnitude of an infinitesimal displacement is \(ds=\|d\vec{r}\|\). The magnitude \(ds\) represents an infinitesimal length. To get a total length, we need to add up infinitely many infinitesimal lengths; in other words, we need to integrate.
The text discusses length of curve from a point of view that does not emphasize infinitesimal displacement vectors. In class we'll make use of infinitesimal displacment vectors in a variety of contexts so I encourage you to think through Section 11.3 problems using infinitesimal displacement vectors rather than substituting into a formula such as the one on page 678 of the text.
The writing exercise is due Friday, September 30.
Friday, September 23
Topics: questions on planes problems; paramterizing curves and vector-valued functions
Text: Section 11.1
Tomorrow: questions on 11.1 problems; a bit more on describing curves parametrically; greatest rate of change
Today, we looked at describing curves parametrically. The idea is to give the coordinates for points on the curve in terms of an independent variable, often called the parameter and often denoted t. For a curve in the plane, this means giving x and y in terms of t. For a curve in space, this means giving x, y, and z in terms of t. A curve is a one-dimensional object sitting in two or three dimensions. The parameter t labels each point on the curve with a single value.
We can repackage a parametric description of a curve as a vector-valued function in the form \[ \vec{r}(t)=x(t)\,\hat\imath+y(t)\,\hat\jmath \] for curves in the plane or \[ \vec{r}(t)=x(t)\,\hat\imath+y(t)\,\hat\jmath+z(t)\,\hat k \] for curves in space. Each input of \(\vec{r}\) is a single real number \(t\) and each output is a vector \(x\,\hat\imath+y\,\hat\jmath+z\,\hat k\). Alternatively, we can think of the output as an ordered triple \((x,y,z)\).
In terms of calculus, we can compute the derivative \(\vec{r}^\prime\) of a vector-valued function by differentiating each component with respect to t. If we think of \(\vec{r}\) as giving the position of an object moving in time \(t\), then the derivative \(\vec{r}^\prime\) is the velocity of the object. The second derivative \(\vec{r}^{\prime\prime}\) is the acceleration of the object.
The writing exercise is due Friday, September 30.
Thursday, September 22
Topics: questions on Section 10.3 problems; point-normal form for the equation of a plane
Text: Planes handout 2 and (optionally) Section 10.5
Tomorrow: questions on planes problems; describing curves in space
The main idea we discussed in class is what we will call the point-normal form for the equation of a line. The starting point for this equation is to consider specifying a plane by giving a point on the plane and a vector perpendicular to the plane. Such a vector is called a normal vector. There are details on this in Section 10.5 but these are mixed in with several other ideas so I have pulled out the main idea we want on this handout. The handout includes the assigned homework problems.
We will skip over the ideas in Section 10.4 (on what is called the cross product) for now. We'll come back to these ideas later in course when we need them.
The writing exercise is due Friday, September 30.
Tuesday, September 20
Topics: writing exercise assignment; more on dot product
Text: Section 10.3
Tomorrow: questions on Section 10.3 problems; point-normal form for the equation of a plane
Our first topic today was a quick comment about unit vectors and unit coordinate vectors. A unit vector contains information about the direction of a vector. The unit coordinate vectors are the special unit vectors pointing in the directions of the positive coordinate axes.
We then returned to our discussion of the dot product. In terms of components, the dot product is given by \[\vec{u}\cdot\vec{v}=u_x v_x+u_y v_y+u_z v_z.\] In terms of geometry, the dot product is given by \[ \vec{u}\cdot\vec{v}=\|\vec{u}\|\,\|\vec{v}\|\cos\theta\] where \(\theta\) is the angle between the two vectors. In many situations, you will want to think geometrically (using the second expression) and then compute in terms of components (using the first expression). We looked at some algebraic properties to see that the dot product does act like a multiplication in that it commutes and it distributes over vector addition. The dot product provides an efficient way to compute the angle between two vectors and to compute the projection (a vector) or component (a number) of one vector along the direction of another vector.
Monday, September 19
Topics: questions on Section 10.2 problems; angle between two vectors and the dot product; return Exam #1
Text: Section 10.3
Tomorrow: more on dot product
In class, we looked at the question of how to compute the angle between two vectors in terms of the vector components. Using the law of cosines and a bit of algebra, we found that the angle \(\theta\) is given by \[ \cos\theta=\frac{u_x v_x+u_y v_y+u_z v_z}{\|u\|\|v\|}. \] We will find it convenient to name the expression in the numerator. We will call this the dot product of \(\vec{u}\) and \(\vec{v}\) and denote this by \[ \vec{u}\cdot\vec{v}=u_x v_x+u_y v_y+u_z v_z. \] Tomorrow, we'll work with the dot product to understand its properties and uses. We will see that it is a way of multiplying two vectors (to get a number) in the sense that it obeys familiar algebraic properties such as distributing over vector addition.
I have assigned problems from Section 10.3 as a preview. You can wait until after class on Tuesday to look at these.
Friday, September 16
Topics: previewing greatest rate of change; vectors
Text: Section 10.2
Tomorrow: questions on Section 10.2 problems; angle between two vectors and the dot product
We started class by previewing an idea we'll spend more time with later, namely direction and size of the greatest rate of change in a function of more than one variable. Before we return to this idea in detail, we'll develop some basic mastery of vectors as a tool for describing quantities that have both direction and size.
Today, we began talking about vectors using displacements as an example. We gave geometric definitions of what it means to add and scale vectors. We then introduce a cartesian coordinate system so that we could add and scale vectors using components. You should work on learning to think about vectors both geometrically and in terms of components. In many situations, we will think geometrically to in order to set up the relevant vector operations and we will then carry out those operations using components. Once we have carried out the operations, we can again think geometrically to interpret the result.
Thursday, September 15
Topics: Exam #1
Text: Sections 9.4, 10.1, 10.6, planes handout, 12.1-12.4
Tomorrow: previewing greatest rate of change; vectors
Tuesday, September 13
Topics: exam overview; questions on Section 12.4 problems
Text: Sections 9.4, 10.1, 10.6, planes handout, 12.1-12.4
Tomorrow: Exam #1
Exam #1 will be on Thursday, September 15. We will use the 80 minute period from 8:00 to 9:20. The exam will cover material from Sections 9.4, 10.1, 10.6, 12.1-12.4, and the handout on planes. This handout has a list of specific objectives for the exam. You might also want to look at questions from old exams. Since we have covered the material in a different order than previous course offerings, I have put together this composite of Exams #1 and #2 from Spring 2011.
I will be available for office hour today (Tuesday) from 12:30 to 1:30 and for appointments after that until at least 4:30. On Wednesday, I will time in the late morning and after 2:00. If you have questions, email or call to set up a time to talk. I can address questions sent by email.
I have reserved TH 381 (next to our usual classroom) starting at 7 pm on Wednesday September 14 for an informal Math 280 study session. If you are looking for others to study with, come to the classroom after 7 pm and find a small group working on something of interest.
Also remember that tutors are available in the Center for Writing, Learning, and Teaching and in TH 390.
Monday, September 12
Topics: questions on 12.4 problems; exam overview
Text: Section 12.4
Tomorrow: questions on 12.4 problems; exam overview
In class, we looked at an example of a chain rule involving partial derivatives. Chain rules are relevant when differentiating functions that are compositions of other functions. In the context of functions of more than one variable, there are many ways to build compositions so there are many chain rules. Rather than trying to memorize a chain rule for each specific type of composition, you should work to understand how the pieces of a chain rule fit together in general. The text shows how to use tree diagrams as one way of doing this.
Exam #1 will be on Thursday, September 15. We will use the 80 minute period from 8:00 to 9:20. The exam will cover material from Sections 9.4, 10.1, 10.6, 12.1-12.4, and the handout on planes. This handout has a list of specific objectives for the exam. You might also want to look at questions from old exams. Since we have covered the material in a different order than previous course offerings, I have put together this composite of Exams #1 and #2 from Spring 2011.
I have reserved TH 381 (next to our usual classroom) starting at 7 pm on Wednesday September 14 for an informal Math 280 study session. If you are looking for others to study with, come to the classroom after 7 pm and find a small group working on something of interest.
Friday, September 9
Topics: questions on 12.2 problems; rate of change for functions of two or more variables
Text: Section 12.3
Tomorrow: questions on 12.3 problems; chain rules involving partial derivatives
In class, we looked at rates of change for a function of two variables. As example, we used the relationship between T, p, and V given by the ideal gas law. Using a plot of level curves for T in the Vp-plane, we thought about
- rate of change in T with respect to V (with p held constant), and
- rate of change in T with respect to p (with V held constant)
for two different points. We estimated some runs and corresponding rises to estimate rates of change.
To get exact values for these rates of change rather than estimates, we turn to differentiation. Specifically, a partial derivative gives us the rate of change in the output variable with respect to one of the input variables with all other input variables held constant.
Your main goal for the weekend should be to work on becomcing proficient with the mechanics of computing partial derivatives. I've assigned (a lot) of problems from Section 12.3 so that you can master these mechanics. You'll need to recall all of your differentiation techniques from first-semester calculus and you'll need to keep the right mindset.
Exam #1 will be on Thursday, September 15. If possible, we will use the 80 minute period from 8:00 to 9:20. If you have not already replied to my email asking whether or not this works for your schedule, please do so as soon as possible.
Thursday, September 8
Topics: questions on 12.1 problems; continuity and discontinuities; limits
Text: Section 12.2
Tomorrow: questions on 12.2 problems; rate of change for functions of two or more variables
Limit is a fundamental idea in calculus. Today, we looked at generalizing the limit idea from the familiar context of functions of one variable to our new context of functions of more than one variable. For a function of one variable, we sometimes analyze a limit by looking at the limit from the left and the limit from the right. With a function of more than one variable, there are many paths to the limit point. For each, we can look at the path limit. If any two path limits differ, we can conclude that the overall limit does not exist. If all of the path limits we examine agree, we might conjecture that their common value is the overall limit. To prove such a conjecture, we would need to make additional arguments. For example, we might be able to algebraically manipulate the function to get a form for which the limit is obvious. One use of limit comes in defining continuity : a function is continuous for a specific point if the limit of a function at that point is equal to the output of the function at that point.
Exam #1 will be on Thursday, September 15. If possible, we will use the 80 minute period from 8:00 to 9:20. If you have not already replied to my email asking whether or not this works for your schedule, please do so as soon as possible.
Tuesday, September 6
Topics: questions on Section 10.6 problems; functions of two or more variables
Text: Section 12.1
Tomorrow: questions on 12.1 problems; continuity and discontinuities; limits
Our next focus in the course will be functions of several variables. We started today by looking at examples of functions of two variables. The usual ideas of function are relevant: domain, range, and graph. Building or visualizing a graph requires thinking in three dimensions since we need two coordinates for the inputs (x,y) and one coordinate for the output z=f(x,y). One approach to is to sketch level sets (a.ka. contours) in the input plane. A level set is the set of points (often a curve) in the input plane on which the output has a constant value.
For functions of three variables, we can think about domain and range. The graph of a function of three variables requires thinking in four dimensions, which we will not do directly. We can, however, draw or visualize level sets. In this context, a level set is the set of points (often a surface) in the input space on which the output has a constant value.
Exam #1 will be on Thursday, September 15. If possible, we will use the 80 minute period from 8:00 to 9:20. If you have not already replied to my email asking whether or not this works for your schedule, please do so as soon as possible.
Friday, September 2
Topics: questions on Section 9.4 problems; quadric surfaces
Text: Section 10.6
Tomorrow: questions on Section 10.6 problems; functions of two variables
Our focus in class today was quadric surfaces. There is a brief catalog of these on page 655 of the text. We looked at a few examples in class; you'll need to explore the others on your own as you look at homework problems. Rather than trying to memorize the catalog on page 655, it is more important to master the ability to look at cross-sections and then see how those fit into a surface. Learning the names of these quadric surfaces is helpful so you can communicate more effectively.
You can view some interactive three-dimensional pictures (similar to ones we looked at it class) at the 3D Picture Gallery.
If you are interested in improving your sketchs of quadric surfaces, you might find this handout from Sinclair Community College to be helpful.
Thursday, September 1
Topics: questions on planes handout problems; ellipses, parabolas, and hyperbolas (a.k.a. conic sections)
Text: Section 9.4
Tomorrow: questions on Section 9.4 problems; quadric surfaces
In class, we reviewed some basics of ellipses, parabolas, and hyperbolas. In particular, we started from a purely geometric definition for each type of curve and then introduced a coordinate system to get an analytic description. In all three cases, the analytic description is a quadratic equation in two variables. As a small challenge, you can fill in the steps that we skipped over between the geometric definition and the most common form of an analytic description for an ellipse and for a hyperbola.
We can also turn this around and ask about the graph of any quadratic equation in two variables. It is a fact that the graph of any quadratic equation in two variables is an ellipse, a parabola, or a hyperbola. That is, the graph of any equation of the form
\[ Ax^2+2Bxy+Cy^2+Dx+Ey+F=0\qquad A,B,C\textrm{ not all zero} \]
is an ellipse, a parabola, or a hyperbola. You can determine which type of curve by computing \(AC-B^2\). If this quantity is positive, the graph is an ellipse. If this quantity is zero and one of D or E is nonzero, the graph is a parabola. If this quantity is negative, the graph is a hyperbola.
Tomorrow, we will bump these ideas up to three-dimensions so we will be dealing with quadratic equations in three variables and the corresponding graphs that are surfaces in space.
Tuesday, August 30
Topics: questions on Section 10.1 problems; equations of planes
Text: Planes handout
Tomorrow: questions on planes handout problems; ellipses, parabolas, and hyperbolas (a.k.a. conic sections)
In class, we looked at equations of planes. In the text, this material is covered in Section 10.5 using some ideas we have not yet developed. We will get to those ideas later in the course, but for now you can use this handout on equations of planes. All of the ideas here are natural generalizations of equations of lines in a plane.
On this course page, I will sometimes use typeset mathematical expressions using a system called MathJax. As an example, the quadratic formula is \[ x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}. \] Does the line above show a nicely formatted expression? If not, please send me a quick note telling me what platform (device, operating system, browser) you are using.
Monday, August 29
Topics: course logistics; functions of more than one variable; points, lines, and planes in space
Text: Section 10.1
Tomorrow: questions on Section 10.1 problems; planes, spheres and other surfaces in space
In class, we began exploring three-dimensional space using cartesian coordinates. We first looked at the graph of a function of two variables, specifically z=x2y3, and then at some simpler geometric objects (such as planes). You should start working on the assigned problems from Section 10.1. As part of this, you will need to read Section 10.1 about equations of spheres in space. This is a straightforward generalization of equations of circles in a plane.
Here is an interactive plot of the function graph we looked at in class. You can rotate and zoom to look at this from various perspectives.
To get some sense of what is expected in terms of the prerequisite courses in the calculus sequence, you might find it useful to look at this Math 180 final exam and at this Math 181 final exam from the most recent times I have taught each of these courses.