| Section | Problems to do | Submit | Target or due date | Comments |
|---|---|---|---|---|
| 9.1 | 1-45 odd | 14,42 | Friday, September 1 | |
| 9.2 | 1-7 odd, 17-27 odd, 35-47 odd | 44,48 | Wednesday, September 6 | |
| 9.3 | 1-19 odd,23,29,37,51 | 16,36 | Thursday, September 7 | |
| 9.6 | 5,9,11,15 | None | Friday, September 8 | |
| 9.4 | 5,9,15,17,21,25,27,29,31,37,39,45 | 18,36 | Monday, September 11 | |
| 9.5 | 17,19,21,25,27,29,31,33,47 | None | Wednesday, September 13 | |
| 9.6 | 19,21,23,27,31,35,37,47,55,56 | None | Wednesday, September 13 | |
| 9.4 | 55,56,57 | None | Thursday, September 14 | |
| 9.2 | 13,29,31 | None | Wednesday, September 20 | |
| 9.7 | 3-23 odd, 31 | 16,38 | Thursday, September 21 | |
| 9.5 | 1-11 odd,15,39,41,45,55 | 16,54 | Monday, September 25 | |
| 10.1 | 1,9,11,13,17,21,23,27,35,37,41,45,49,57 | 44,58 | Wednesday, September 27 | |
| 10.2 | 1,3,7,9,15,17,19,21,23 | None | Wednesday, September 27 | |
| 10.2 | 27,31,35,43,45,51,59,61 | 36,58 | Friday, September 29 | |
| 10.3 | 15,17,40 | None | Friday, September 29 | |
| 11.1 | 1,5,7,11,13,17,35-40,53,57 | 54,58 | Wednesday, October 4 | |
| 11.2 | 3,5,7,11,15,19,31,33,35,39 | 18,30 | Friday, October 6 | |
| 11.3 | 3-21 odd, 23,27,43,45,47,53 | 42,48 | Monday, October 9 | |
| 11.4 | 1,3,7,13,17,27,29,31,37,43 | None | Wednesday, October 11 | |
| 11.6 | 1-9 odd,13,15 25-33 odd,39,41,43,45,47,53,63 | 46,58 | Monday, October 23 | |
| 11.5 | 5,9,13,17,21,37,43,53 | 34,52 | Wednesday, October 25 | |
| 11.7 | 9,13,15,21,25,27,29,35,39,45,57 | 20,Box problem | Monday, October 30 | |
| 12.1 | 15,17,19,23,25,29,31,39 | 36,38 | Friday, November 3 | |
| 12.2 | 21,23,25,27,31,39,53,57 | 28,52 | Friday, November 3 | |
| 6.3 | 3,11,19,23,27 | None | Monday, November 6 | |
| 12.3 | 1,11,13,17,27,33,37,39,45,49,55,59 | None | Wednesday, November 8 | |
| 12.5 | 5,7,11,17,19,27,31,39, | 32,48 | Wednesday, November 15 | |
| 12.7 | 3,5,7,11,15,17,23,39,43a,47,49,51,53,63 | 40,56 | Thursday, November 16 | |
| 6.4 | 3,17,27 | None | Friday, November 17 | |
| 13.2 | 3,5,31,37 | None | Friday, November 17 | |
| 12.4 | 3,7,15,19,27,43 | None | Monday, November 20 | |
| 13.5 | 1,5,9,17,39 | None | Monday, November 20 | |
| 13.2 | 7,13,21,25 | None | Wednesday, November 29 | |
| 13.5 | 23,29,35 | None | Wednesday, November 29 | |
| 13.1 | 3,9,17,23,35 | None | Thursday, November 30 | |
| 13.3 | 5,9,13,17,27,33,35,45 | None | Monday, December 4 |
After class, Megan pointed out an error I made at the end of Section 13.3 #45. For an antiderivative of u-3/2, I wrote down (-1/2)u-1/2. This should be -2u-1/2. With this, the correct final result is V=KmM/r rather than V=KmM/(4r).
Exam #4 will be on Wednesday from 9:00-9:50. The focus will be on material we have covered since the previous exam. This includes material from Sections 12.5, 12.7, 6.4/13.2, 12.4/13.5, 13.1, and 13.3 (in the order we covered the material). In terms of goals for Exam #4, a well-prepared student should be able to
In terms of specific objectives for Exam #4, a well-prepared student should be able to
In discussing potential functions and conservative vector fields, I omitted some technical details on continuity of the functions. In particular, to apply the ∇×F=0 test to determine if F has a potential function, we need to require that F and ∇×F are continuous in a simply-connected region of space. A region of space is connected if each pair of points in the region can be connected by a continuous curve that contains only points in the region. Informally, this means the region is one big "blob" and not two (or more) disconnected "blobs". A region of space is simply-connected if it is connected and if every closed loop in the region can be continuously shrunk to a point while remaining in the region. A solid sphere is simply-connected. The region consisting of all space with one point removed is simply-connected. The region consisting of all space with one line (the entire line) removed is connected but not simply-connected. Likewise, a solid torus is connected but not simply-connected.
The text also defines the idea of path independence of line integrals for vector fields. This is intimately related to the existence of a potential function and conservative vector fields. Suppose a given vector field F has a potential function V for a region of space. Consider two points P and Q in that region of space. Let C1 be one curve in the region starting at P and ending at Q. Let C2 be some other curve in the region with the same start point and the same end point. Since the Fundamental Theorem applies and the value of V(Q)-V(P) doesn't care about the curves, the line integral of F for C1 and the line integral of F for C2 are equal (with both equal to V(Q)-V(P)). The property of line integrals for a given vector field being equal for all curves that have the same start point and the same end point is called path independence.
Exam #4 will be on Wednesday, December 6. It will focus on material we have covered since the previous exam. This includes material from Sections 12.5, 12.7, 6.4/13.2, 12.4/13.5, 13.1, and 13.3 (in the order we covered the material). I will post more detail goals and objectives sometime over the weekend.
For your reference, here's the interpretations of divergence and curl that we talked about in class today: Think of the vector field outputs as velocity vectors for a fluid flow. Imagine placing a drop of dye in the fluid.
I'm not assigning additional problems today. You can take this opportunity to catch up on mastering the mechanics of computing line integrals, surface integrals, divergence, and curl.
In class today, I introduced the divergence and curl of a vector field in terms of computing partial derivatives in cartesian coordinates. This gives us an easy way to compute but makes doesn't tell us much about what divergence and curl mean. For the homework problems I've assigned from Section 13.1, focus on mastering the mechanics of computing divergence and curl. We'll spend some time tomorrow trying to understand what the divergence and curl of a vector field tell about the vector field.
Exam #4 will be Wednesday, December 6. The focus will be material from Chapter 13 on the calculus of vector fields.
I've assigned problems from Sections 13.2 and 13.5 that deal with line integrals and surface integrals for vector fields. I'll post a few more comments on these ideas later this afternoon or early this evening.
In class, I distributed a handout with notes on line integrals. You'll probably want to read through this before trying the assigned problems from Section 13.2 The notes on notation should help you read the text's notation.
I forgot to distribute a similar handout with notes on surface integrals. You might want to read this before working trying the assigned problems from Section 13.5. I'll bring these to class on Wednesday so you don't need to print a copy if don't want. Here's a 3D version of one figure from the handout. (I think I reversed the meaning of the vector colors in this from the handout. I'll check on this latter.)
In defining surface integrals for vector fields, I mentioned that the surface must be oriented but didn't fill in the details on what this means. In order for a surface to be oriented, it must first be two-sided rather than one-sided. A Mobius strip is an example of a one-sided surface. Planes (or pieces of planes), graphs of functions, spheres, and cylinders are examples of two-sided surfaces. For each of these, you can unambiguously identify two sides. For a two-sided surface, you can color one side red and the other side blue with no ambiguity. What happens if you try coloring a Mobius strip with two colors? So, we will focus our attention on two-sided surfaces. To orient a two sided surface means to set up area elements vectors dA to all "point on the same side of the surface." For example, on a sphere, we can orient the area element vectors to all be pointing outward or to all be pointing inward. Either choice gives us an oriented surface. If we choose some area element vectors to point outward and others to point inward, the result is not an oriented surface.
In class, I will emphasize a fluid flow interpretation of vectors fields. Think of the vector field V as giving the velocity of fluid at each point in space (or in the plane if we restrict attention to two dimensions). With this we have the following interpretations:
Vector fields are introduced in Section 13.1 of the text. Most of Section 13.1 deals with the differential calculus of vector fields. I plan to deal with these ideas after we have talked about line integrals for vector fields (Section 13.2) and surface integrals for vector fields (Section 13.5).
I have not assigned problems from Section 13.1. Your assignment for today is to check out the Vector Field Analyzer (written by Matthias Kawski of the Mathematics Department at Arizona State University ). This Java applet allows you to plot and analyze a two-dimensional vector field. Be patient as the page loads; it takes a minute or two for the Java code to set everything up. After the code is loaded, you will see a plot of the default vector field. To plot a different vector field, enter the components of the vector field you want in the boxes near the bottom of the applet window and then click on the button "Plot this field." You should try the simple examples we have looked at in class such as F=x i+y j and F=-y i+ x j . The Vector Field Analyzer has lots of features (and a few bugs).
One feature you should play with is based on thinking of vector field outputs as velocity vectors for fluid flow. Click on the tab labeled "DEs/flows." This part of the program lets you draw a box on the vector field plot and then watch as the box "goes with the flow."
We have seen one important type of vector fields earlier in the course. Given a function f(x,y), we can think about or compute its gradient vector field &nablaf. We can turn this around: Given a vector field F, we can ask if that vector field is the gradient of some function. That is, for a given vector field F, can we find a function f such that ∇f=F?. This question should should familiar. If there is such a function f, it is called a potential function for the vector field F.
Suppose we have a planar vector field F. We want to think about whether F has a potential function or not. By definition, the function f is a potential function for F if ∇f=F. Recall that at a point P(x,y), the gradient vector ∇f(x,y) is perpendicular to the level curve of f that goes through P. If we have a plot of the given vector field F, we can start by drawing, at the base of each vector, a short line segment perpendicular to that vector. The question we have to ask is Can we connect these line segments to form level curves for the potential function f? The level curves of a function can not intersect. (You should think through why this is so.)
To test out this idea, draw a vector field plot for each of the vector fields F=x i+y j and F=-y i+ x j . On each vector field plot, draw the perpendicular line segments and see if you can connect these up to form sensible level curves.
The Vector Field Analyzer provides some tools to help with this geometric view of potential functions. The first is right above the ``Plot this field'' button. You will see the phrases ``Arrows (contra-var)'' and ``Stacks (co-var).'' The default is ``Arrows''. Click on the button closest to ``Stacks'' and look for the change in the plot window. Each arrow is replaced by a ``stack'' of line segments perpendicular to the corresponding arrow. The density of the stack is proportional to the length of the corresponding arrow. To make this a little more obvious, you might want to change the value in the box labeled ``grid'' just under the second component window near the bottom. The default value is 20 meaning that arrows/stacks are plotted on a 20 by 20 grid for a total of 400 arrows/stack. If you change this value to 10 (and then hit the ``Plot this field'' button), you get a 10 by 10 grid. With fewer arrows/stacks, each can be bigger without overlap. These stacks represent pieces of potential level curves. Can these be joined up into sensible level curves? Try the vector fields F=x i+y j and F=-y i+ x j .
The second tool is under the ``DEs/flows'' tab. On this tab, click on the button labeled ``Equipot. candidates.'' Then, click on one or more points inside the plot window. A blue dot will be drawn at each point on which click in the window. Finally, click on the button labeled ``Stop and Go.'' For each point you made, the program will start drawing a curve that is perpendicular to the vector field arrows (and parallel to the stacks if you are in that view). Experiment here with the same two vector fields used above.
So far, we have been looking at line integrals and surface integrals for scalar-output functions. Next week, we will begin a study of vector fields and then look at line integrals and surface integrals for vector fields. Here's an outline (with connections to the text) for the chunk of material we are currently looking at:
For the area element in surface integrals, we are using dA in class while the text uses dS. There are at least two ways you can come up with a valid expression for the area element dA in the coordinate system you choose:
I am late in posting a homework assignment. I'll see how many questions you have in class tomorrow on the assigned problems. If I sense people didn't have enough time to look at these, I'll also address questions from these on Monday.
In class, we looked at examples of computing line integrals for scalar-output functions. A better name for these would be curve integrals but we're stuck with line integrals for historic reasons. In class, we used the notation dl to denote the length of a small piece of the curve. The text uses ds. I've assigned problems from Section 6.4 (which deal with computing the length of a curve) and problems from Section 13.2. I'll assign more problems from Section 13.2 after we talk about a different flavor of line integrals, namely those that involve vector fields.
We also started talking about surface integrals for scalar-output functions. We'll continue with this tomorrow. These ideas are discussed in Section 12.4 and the first part of Section 13.5 in the text. (Section 12.4 deals with computing the area of a surface so it is analogous to Section 6.4 on computing the length of a curve.)
I have assigned additional problems from Section 12.7 to include problems that deal with spherical coordinates.
In class, we did not finish writing down the volume element in spherical coordinates. You can come up with the correct expression by doing the worksheet I distributed in class. You can work on the assigned problems from Section 12.7 even if you can't come up with the correct volume element on your own. The correct expression is given in the text on p. 838.
The picture accompanying Section 12.7 #63 is not very good. I'll try to post a better picture this evening.
We are skipping over the material in Section 12.4 for now. We'll come back to it soon. We've been talking about one of the ideas from Section 12.6 all along, namely getting a total for some quantity from a density for that quantity. We won't do anything more from the material in Section 12.6.
Cylindrical and spherical coordinates are covered in Section 12.7. We have talked about cylindrical coordinates so I've assigned from relevant problems from Section 12.7. (For the first few problems, just do the part that concerns cylindrical coordinates.) I'll assign more problems from this section after class on Monday.
Spherical coordinates consist of one distance and two angles. In reference to a cartesian coordinate system, these are
At the end of class, Andy pointed out that I might have written down an incorrect antiderivative for cos2(3θ). He was right. A correct antiderivative is θ/2+sin(6θ)/12 rather than θ/2+sin(3θ)/12. (That is, the argument of the sine function should be 6θ rather than 3θ.) Using this gives the correct final result of (4π/3)σo. The area of the petal is thus 4π/3.
Exam #3 will be on Thursday from 9:30-10:50. The focus will be on material we have covered since the previous exam. This includes material from Sections 11.5 to 11.7 and 12.1 to 12.3. In terms of goals for Exam #3, a well-prepared student should be able to
In terms of specific objectives for Exam #3, a well-prepared student should be able to
Polar coordinates are covered in Section 6.3 of our text. This material falls into Math 181 so I covered it quickly in class today. Come talk with me outside of class if you need more time with these ideas. I've assigned some problems from Section 6.3.
You should figure out how to use your calculator to plot polar curves. On a TI-83/84/86, you first set the graph mode to "Pol" under the MODE menu. Also make sure your calculator is in radian mode. In "Pol" mode, the function entry screen will show "r1=". This is where you type in a formula for r as a function of θ. You may also need to adjust the values of θMin, θMax, and θStep. Finally, you may want to choose ZSQR from the ZOOM menu to get an aspect ratio of 1 so that circles look like circles rather than ellipses.
I've also assigned problems from Section 12.3. You can start looking at these now or you can wait until after class on Monday. We'll do a few examples on Monday.
Exam #3 will be Thursday, November 9 from 9:30 to 10:50. The focus will be on material we have covered since the previous exam.
You will notice that in class and in the text, we make a distinction between double integrals and iterated integrals. Double integrals are defined as limits of Riemann sums. Iterated integrals are defined as doing one integration inside another, treating the outer variable of integration as constant when doing the inner integration. This distinction between double integral and iterated integral is blurred by the fact that each double integral has the same value as a certain iterated integral (with respect to a particular coordinate system). This equality of values is the content of Fubini's theorem on page 781 and 788 of the text.
For most of the problems I have assigned from Sections 12.1 and 12.2, you will be focussed on the mechanics of evaluating double integrals (by evaluating the related iterated integral). You should also keep some interpretation in mind either by thinking of the integrand as a density function or by thinking of computing the signed volume of a region of space.
In class, we set up one example of a triple integral and then evaluated the integral by evaluating the related iterated integral. Triple integrals are discussed in Section 12.5 of the text. I'll assign problems from this material later.
So far, we've used cartesian coordinates to set up our iterated integrals. For some regions of integration, it will be convenient to use an alternate coordinate system. We'll look at polar coordinates for regions in the plane (Section 12.3). For regions in space, we'll look at cylindrical coordinates and spherical coordinates (Section 12.7).
In class, we talked about going from density for some quantity (mass, charge, cost) to a total for that quantity. For a constant density, this is simply a matter of multiplication. For a nonconstant density, we end up with an integral. If we have a length density, the integral is a familiar definite integral for a function of one variable. For an area density, we will end up with a double (definite) integral for a function of two variables. For a volume density, we will end up with a triple (definite) integral for a function of three variables. In general, going from density to total is one application of multiple integration, the topic of Chapter 12.
I have not yet assigned problems from Section 12.1. You can focus on your project between now and class on Wednesday.
I've added Problems 25,27, and 29 to the assignment for Section 11.7. These deal with global (aka absolute) extrema.
Here's a 3d graphics showing the graph of the function f(x,y)=8x3-24xy+y3 for -1≤x≤3 and -1≤y≤5. This is the function we looked at as an example of finding global extrema.
For homework to submit for Section 11.7, you should finish up with the problem we started in class. For reference, here's the problem:
Consider the problem of designing a box to meet certain specifications at minimum cost. The design specifications call for a rectangular box of total volume V (in cm3). The box is to be constructed with material for the top that costs a (in dollars per cm2), material for the bottom that costs b (in dollars per cm2), and material for the sides that costs c (in dollars per cm2). Find the dimensions of the box that meets the specifications at minimum cost.
In class I use the phrase local maximum or minimum while the text uses relative maximum or minimum. In a similar fashion, I will use global maximum or minimum while the text uses absolute maximum or minimum.
I've assigned problems from Section 11.7 that deal with finding and classifying local extrema. I'll assign additional problems tomorrow after we have talked about global extrema and about applications.
I haven't yet assigned problems from Section 11.7 since we just got started on this material.
One context in which chain rules are used is in changing from one
coordinate system to another coordinate system. Problem 8 in Section 11.5
provides an example of this. You can think of x and y as one
set of cartesian coordinates and u and v as a second set of
cartesian coordinates. To see the relation between these coordinate
systems, draw a set of coordinate axes for x and y. Curves
of x= constant are vertical lines while curves of y= constant
are horizontal lines. These make up the coordinate grid for the
xy-coordinate system. The xy-coordinates are related to the
uv-coordinates by
x=u+v and y=u-v
or, by solving,
u=(x+y)/2 and v=(x-y)/2.
Now look at curves of u= constant. These are lines of slope -1 in
the xy-coordinate system. Likewise, curves of u= constant
are lines of slope +1. These lines make up the coordinate grid for the
uv-coordinate system. The uv-coordinate system is rotated by
90° with respect to the xy-coordinate system. Problem 34 deals
with yet another coordinate system, namely polar coordinates given
by r and θ. (Note that you don't need to understand
the geomtry of polar coordinates in order to do the calculations required
for Problem 34.)
I've included some new problems in the assignment for Section 11.6. The complete asssignment is given above. The new problems for Section 11.6 are #13,15,39,41,43,53,63.
For problems such as 53, the idea is to think of the given equation as defining a level surface of a function. For example, in 53(a), you can take the function to be f(x,y,z)=x2/a2+y2/b2+z2/c2. (Note that x,y,and z are the input variables while a,b, and c are constants.) The key idea is that each gradient vector of f is perpendicular to a level surface for f. Thus, at a particular point, the gradient vector is a normal vector for the plane tangent to the level surface at that point. (Read that last sentence repeatedly until it makes sense.)
In class, we started with the Greatest rate of change handout to get a geometric idea of gradient vectors. We then used what we know about differentials to get a component formula for gradient vectors.
I've skipped over the material in Section 11.5 for now. In Section 11.6, we're working with material on gradient vectors (see page 739) before dealing with directional derivatives. (We did talk about directional derivatives, but not by name and not in detail.) I've assigned a few problems from Section 11.6 and will assign more tomorrow.
Have a great Fall Break.
Exam #1 will be Thursday, October 12 from 9:30 to 10:50. It will cover everything we have done so far this semester with emphasis on material we have covered since the last exam. This includes material from Sections 9.2, 9.7, and 9.5, Sections 10.1-10.3, and Sections 11.1-11.4. In terms of goals for Exam #2, a well-prepared student should be able to
In terms of specific objectives for Exam #2, a well-prepared student should be able to
You might want to check out this nice interactive 3d graphic of a tangent plane. You'll need to scroll down the linked page a bit to see the graphic.
I've posted an assignment from Section 11.4 but I don't expect you to do much on it before Monday since we just starting talking about the relevant topics.
Exam #2 will be Thursday, October 12 from 9:30-10:50. It will cover material through Section 11.4. Please check your schedule for this day and let me know if you have a conflict that prevents you from staying until 10:50.
I've reorganized this web page a bit because the movies and graphics were increasing the loading time. I've now put each movie on a separate page with a link from this page. I've also created a list of all the movies and graphics in the Fun Stuff section (because they are fun, right?).
Before you read Section 11.3 or start the homework, you should finish computing all of the first and second partial derivatives for f(x,y)=xcos(xy). When you are done, look for an interesting relationship between two of the second partial derivatives. (If you don't see an interesting relationship, check your calculations).
In class, we talked about parametrizing the curve given in Section 10.1 Problem 44. I drew a pretty pathetic picture of this. To make up for that, I put together a 3d graphic of the surfaces and curve.
News flash: Our move has been delayed so I will be in my current office (Thompson 321D) through next Monday, October 9.
In class, we did not get to an example illustrating the idea of looking at limits along paths so I've moved the due date for homework from Section 11.2 to Friday.
Section 11.1 Problems 35-40 ask you to match level curve plots with surface plots. Some of the level curve plots are a bit shaky. This is actually typical of level curve plots generated by technology. Plotting level curves is really a game of "connect-the-dots". It's easy to make the wrong connections, particularly if the function outputs change rapidly.
We have begun studying a new type of function. For a function of this type, each input is an ordered pair (x,y) of real numbers and each output f(x,y) is a real number. The graph of such a function is the set of all points with coordinates (x,y,f(x,y)). Typically, the graph will be a surface in space. (For a function with lots of discontinuities, the graph might be a bunch of disconnected points.)
In Section 10.3, we will only cover the material in the first subsection "Modeling the Motion of a Projectile in Vacuum". We will skip the rest of Section 10.3 and Sections 10.4-10.5.
I've posted a homework assignment for Section 10.2. After class on Wednesday, I'll assign more problems from this section, including some to be turned in.
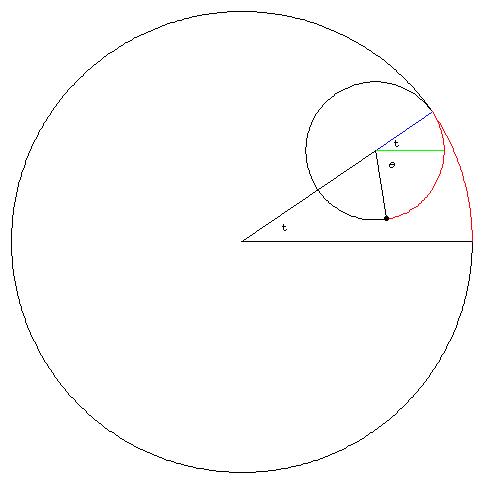
Here's how to think about the part of Section 9.5 #55 that I blanked on in class. The figure below shows the geometry of the situation. We are interested in the angle θ since this is how far the point has rotated around the center of the little circle. Notice that this is measured from the horizontal ray, not from the radial ray. From the condition that the little circle is rolling (and not slipping) on the big circle, we know that the arclength corresponding to the angle t on the big circle must equal the arclength corresponding to the angle θ+t on the little circle. Using the fact that arclength is the product of the radius and the angle, we get the equation at=R(θ+t). We solve this equation to get θ=(a-R) t/R.

I've made movies of an epicycloid (Section 9.5 #54) and a hypocycloid (Section 9.5 #55) being traced out.
A few of the assigned problems for Section 10.1 involve things we just started in class today but you should still be able to handle these. When working with vector-output functions, you can do what seems obvious: work with each component one at a time. Working with each component involves doing things from calculus that you are familiar with (computing limits, analyzing continuity, computing derivatives.)
Given a vector-output function F:R→R3, we can draw a curve in space by thinking of each output F(t) as the position vector of a point. In Section 10.1, the text calls this the graph of the function F. I prefer not to use the word graph here because this type of curve differs in important ways from the graph of a scalar-output function. I'll use image curve instead.
I've made movies related to the epicycles example we looked at in class.
To describe a curve in space, we need two or more implicit equations. An alternative is to use a set of parametric equations that give the coordinates (x,y,z) of points on the curve as functions of a single parameter. We can also use this approach to describe curves in the plane. That is, for a curve in the plane, we can choose between a single implicit equation or a set of parametric equations that give the coordinates (x,y) as functions of a single parameter. For example, we can describe the unit circle by the implicit equation x2+y2=1 or by the parametric equations x=cos(t), y=sin(t). A decision on which approach to use depends on the context. Some things are easier to do with implicit equations while others things are easier with parametric equations.
We've looked at planes in space and seen these can be described by linear equations in three variables. We now generalize to surfaces in space. "Curvy" surfaces are described by nonlinear equations.
Exam #1 is tomorrow. Remember that we will meet in Howarth 005. For
additional practice, you can look at the review problems on pages 628-631
of the text. A few of these problems are not relevant because they deal
with material we have not covered. Problems you can ignore are
Proficiency Examination #9,10,19,23,26,32,39,46,47,50
Supplementary Problems #19,23,29,31,32,40,47,51,53,54
Exam #1 will be Friday, September 15 in Howarth 005. It will cover material from Sections 9.1 through 9.6 with the exceptions noted in Monday's note. In terms of goals for Exam #1, a well-prepared student should be able to
In terms of specific objectives for Exam #1, a well-prepared student should be able to
To contact Trevor Kagochi about tutoring at the Peace Community Center, e-mail him at tkagochi@gmail.com.
Exam #1 is on Friday, September 15. It will cover material from Sections 9.1 through 9.6 with the exception of a few subsections:
Our first exam will be next Friday, September 15. We will meet in Howarth 005 for that day only because there is an event for the Race and Pedagogy Conference scheduled in our regular classroom. The exam will cover most of the material in Chapter 9. I'll give you a specific list of things next week.
In Section 9.5, we will cover the first two subsections "Parametric Equations" and "Parametrizing a Curve" after the first exam. In class today, we started looking at the ideas discussed in the third subsection "Lines in R3." We didn't do quite enough for you to do some of the assigned problems. You can leave these until after class on Monday.
Please check your schedule to see if you are available on Thursday, September 14 from 9:30-10:50 so that we can have 80 minutes available for an exam. Send me an e-mail (martinj@ups.edu) if you have a schedule conflict so I can make a decision on the exam date.
In the Section 9.6 problems, you can skip #31 and #37 for now. We'll talk about the ideas you need for these problems in class tomorrow.
In class, we'll be covering the ideas of Chapter 9 in an order that differs from the text. I've introduced planes in space (Section 9.6) and will use this to motivate the cross product (Section 9.4). We'll then generalize from planes to other surfaces (spheres and cylinders in Section 9.2 and quadric surfaces in Section 9.7). Finally, we'll circle back to talk about lines and curves in space (Section 9.5).
We didn't do any examples in class today so I don't yet expect you to do much with the homework assignment from Section 9.6.
In class, I drew a picture of vectors in the plane to support the claim that the dot product distributes over vector addition. Here is a three-dimensional version.
Section 9.2 has some material on equations of spheres and cylinders in space. We haven't yet discussed this in class and none of the assigned problems deal with these ideas. We'll come back to them soon.
We are just getting started on the dot product. Based on what we did in class today, you probably don't have a good (or any) feel for the dot product of two vectors means. You'll develop a feel for this as we see how dot product is used.
If you have not seen vectors before, don't panic if it feels like we are moving rapidly. We will use vectors throughout the course and you will soon be very comfortable with them.
Between now and class on Wednesday, you should focus on recalling the ideas, computational tools, and applications from Calculus I and II. Work on problems from the Calculus I final and Calculus II final I distributed in class. Use the text as a reference. This will be a useful way to familiarize yourself with this text if you haven't used it for previous calculus courses. E-mail, call, or find me if you have questions on any of these problems.
A note on class renumbering: Lower-division mathematics courses were renumbered effective this fall so you will see and hear references to course numbers that are now longer used. In this class, the most relevant courses are
| Course title | New number | Old number |
|---|---|---|
| Calculus and Analytic Geometry I | 180 | 121 |
| Calculus and Analytic Geometry II | 181 | 122 |
| Multivariate Calculus | 280 | 221 |
Links to the movies and graphics from daily notes:
The Mathematical Atlas describes the many fields and subfields of mathematics. The site has numerous links to other interesting and useful sites about mathematics.
If you are interested in the history of mathematics, a good place to start is the History of Mathematics page at the University of St. Andrews, Scotland.
Check out the Astronomy Picture of the Day.
You can look at exams from last time I taught Multivariate Calculus. You can use these to get some idea of how I write exams. Don't assume I am going to write our exams by just making small changes to the old exams. You should also note that we were using a different textbook so some of the notation is different. There are also differences in the material covered on each exam. You can use this old exam to prepare for our exam in whatever way you want. I will not provide solutions for the old exam problems.